Things look rosy. The H-like wave functions above are simple (if we ignore the normalizing constants), and they are the Real McCoy. Unfortunately things get impossibly complicated as soon as we go to a system with two electrons.

In the first place it is tough to visualize ψ for two electrons, because it is a function of 6 positional coordinates (x₁,y₁,z₁,x₂,y₂,z₂), so we'd need 7 dimensions to plot it. I don't know anyone who can visualize 7 dimensions in a concrete way. This is not an insuperable problem, because even if we can't actually visualize ψ, we can think simple thoughts about it. It will be a set of numbers (positive, negative, zero, conceivably even complex) associated with sets of the six coordinates (pairs of positions of the two electrons). It will have a complicated shape such that for any pair of positions the sum of all the (1/m²ψ/ψ) contributions to the kinetic energy will compensate for changes in the potential energy to give a total energy that is independent of positions. ψ²(x₁,y₁,z₁,x₂,y₂,z₂) will be the probability density for Electron 1 to be at (x₁,y₁,z₁) and Electron 2 to be at (x₂,y₂,z₂), both at the same time. If we sum up the probabilities (or integrate ψ²) over all possible pairs of positions, we will get 1.

ψ² is a joint probability, and there is a simple formulation for joint probability that is familiar from flipping coins. The joint probability is often the product of the individual probabilities. If the probability of heads for one coin is 1/2, and the probability of heads for a second is 1/2, then the probability that both are heads is 1/4, that is 1/2 times 1/2. This analogy suggests the possibility that

where AO_A is the H-like wave function (atomic orbital) for Electron 1, and AO_B is the H-like wave function (atomic orbital) for Electron 2. For example, AO_A might be the 1s orbital of a helium atom and AO_B might be its 2p_x orbital. If this were true, we could easily visualize the two-electron atom as a superposition of the electron clouds of two one-electron atoms, and we could write the two-electron wave function as a product of orbitals:

The idea could be extended simply to any number of electrons. The N-electron wave function might just be a product of N orbitals.

Unfortunately this is too good to be true, and herein lies the Main Problem. It is easy to see why multiplying orbitals fails. Joint probability is the product of individual probabilities only when the individual probabilities are independent of one another. This may work for coins, but it surely does not work for electrons that repel one another. The probability that two electrons occupy the same point, or nearby points, at the same time is most assuredly NOT the product of the individual probabilities of each electron being at that point ignoring the other, because the energy due to repulsion would be prohibitively high. Electrons must correlate their motion to avoid one another.

Now we're faced with a tough decision. We can be purists and stick to realistic many-electron functions, which we can't really understand, even if powerful computers can calculate them. Alternatively, we can see whether the product of orbitals might give useful insight into reality, imagining that individual electrons will have more or less the kind of time-average distribution they would have in one-electron problems (except that they tend to avoid on another instantaneously).

Most of the quantitative and qualitative applications of quantum mechanics to atoms and molecules have leaned heavily on the hopeful approximation that a many-electron wave function can be expressed numerically as a product of independent one-electron functions, or orbitals. Efforts are then made to correct for the implicit, and potentially catastrophic, neglect of the influence of electron-electron repulsion, which destroys independence.

The simplest way to try correcting empirically for e-e repulsion is to lower the nuclear charge, using an "effective" Z (Z_eff) instead of the number of protons. Recall that Z appears as a multiplier of r for purposes of converting it to ρ for use in the exponential (e^-ρ/2) of the H-like radial wavefunctions (it also must appear in the normalization constant). Decreasing Z makes ρ change less rapidly with r, and thus allows the electron orbital to spread out, as one would expect if the nuclear charge were reduced (or "screened" by intervening electron density from other electrons). For purposes of calculating an orbital that is mostly near the nucleus, Z_eff should not be much lower than Z, because there is little intervening electron density. For calculating an orbital that is mostly far from the nucleus Z_eff could be quite small, because there would be a lot of intervening density from other electrons. For calculating the He atom a suggested value for Z_eff of the 1s orbital is 1.69 instead of 2. Each 1s electron slightly screens the other. For calculating the 1s orbital of the sodium atom, a value of Z_eff is 10.63, only modestly reduced from the true Z of 11. But for calculating its 2s orbital the value is 6.6, and for the 3s orbital it is only 2.5.

Notice also that for any given principal quantum number, n, the radial distributions of the s, p, d, etc. orbitals are different, so that they should have different amounts of screening by other electrons. This relates to the fact that these sublevels have different energy in many-electron atoms, whereas in a one-electron atom they have the same energy E_n = -RZ²/n². [The difference between the Z_eff values for 2s and 2p of carbon makes sense - the 2s penetrates further toward the nucleus and sees it with less screening. The difference for sodium appears to be in the wrong direction, which may be a sort of error in the method used to describe the orbitals.]

It is obviously pretty crude to estimate repulsion from a wide-ranging electron by treating it as a fractional static electron at the nucleus, but it's better than nothing.

More sophisticated is the Self-Consistent Field (SCF) approach. Each electron is treated in sequence and is assumed to exist in a static electric field. This field is due to the fixed nucleus (or nuclei) and the other electrons, which are not fixed at points, but rather treated as a static cloud of electron density given by superposition of their assumed densities. This potential allows calculating a much improved orbital for the electron in question. One then adds the density from this orbital to the static set and calculates an improved orbital for one of the other electrons. Each orbital is readjusted in turn, again and again, until self consistency is reached and the orbitals stop changing.

Even when self consistency is reached, the answer must be incorrect, since it is obvious that all the electrons are constantly in motion at similar rates (unlike the lethargic nuclei) and tending to stay away from one another. In assuming that all the electrons but one form a static cloud, we don't allow them to avoid one another, and thus we overestimate the e-e repulsion. This error is dignified and concealed from the naive by giving it the name "Correlation Energy". Correlation energy is typically about 0.5% as large as the total energy of an atom, which is small in relative terms, but as large as the energy of a typical bond. (click here for details)

Techniques exist to correct approximately for the dynamic mutual avoidance of electrons (one is called "Configuration Interaction," another is called "Density Functional Theory"), but they are very computationally intensive and are complex beyond simple understanding. With improved computer technology many such calculations are done nowadays for smallish molecules.

As we shall soon see, we are much more often interested in the change in energy between two different arrangements of the same atoms than in the absolute energy of one arrangement. If we were so lucky that the "correlation energy" errors were of about the same magnitude for both atomic arrangements, the errors would cancel out and the difference calculated by ignoring correlation energy would be correct. This is the excuse for thinking the way we do about orbitals.

For our purposes we will use orbitals and will often not mention electron-electron repulsion, but we must remain alert to the type of errors this will entail.

Sometimes an H-like atomic orbital is not correct even for a one-electron atom. For example, if there is an external electron field (due perhaps to another nucleus) in addition to the electron-nuclear attraction, the electron density will tend to shift in one direction. Suppose the field tends to push electrons in the +x direction. One can write an orbital that assigns larger numbers on the +x side of the nucleus, and smaller numbers on the -x side by ADDING 2p_x(x₁,y₁,z₁) to 1s(x₁,y₁,z₁), because the functions have the same sign for +x and opposite signs for -x.  Basing the distorted orbital on the H-like orbitals has the virtue of keeping a shape with lowish kinetic energy (the curvature of the sum of two functions is the sum of their curvatures).

Consider the following hybrid orbital and its probability density:

The first two terms on the right of the density equation denote a superposition of a fraction a² of the 1s orbital density and a fraction b² of the 2p_z density. The last term builds up density for positive x and depletes density for negative x by the same amount. So this hybrid orbital is properly normalized when a² + b² = 1. The ratio of 2p_x to 1s character, b²/a², is in fact the n in the name of an spⁿ hybrid orbital. Different values of n result in different amounts of density shift toward +x. Though you have often heard of sp, sp², and sp³ orbitals, n need not be an integer. It can have any positive value, like 1.63, or 8.09 - whatever does the best job of giving the proper shape to solve the Schrödinger equation. (Click here for demonstration)

Hybrid orbitals are ubiquitous in chemistry, because chemists are interested in situations where there are electric fields due to other nuclei in the vicinity of an atom in question. Physicists, when they are considering isolated atoms, don't care much about hybridization.

Remember that a hybrid orbital is still an orbital, a one-electron wave function.

So far we have dealt with atoms, not molecules. By using orbitals we have been able to treat many-electron atoms (although correlation remains a significant problem for quantitative understanding), but what is to be done when, as chemists, we must deal with many nuclei, that is, with a molecule?

Soon after the invention of quantum mechanics there emerged two limiting viewpoints for understanding the distribution of electrons in molecules. Both approaches are based on the understanding of atoms.

The first view regards the molecule as a gigantic atom with a nucleus that has been fragmented. This "United Atom" model supplies insight into the general shape of orbitals for electrons in molecules. Conceptually this is how computers approach the problem, but it is not very practical for understanding either the details of electron density distribution or the nature of chemical bonding. The second approach begins with separated atoms and their atomic orbitals and attempts to understand the bonding in molecules as resulting from slight changes in the electron distribution as atoms approach one another and interact to form molecules.

From what we know about electron density difference maps from x-ray diffraction, you will not be surprised to know that the separated atom model will provide the most fruitful starting point for understanding bonding.

A molecular orbital (MO) is like a hybrid orbital in being a weighted sum of atomic orbitals (AOs) of the same electron. The difference is that the AOs in an MO can come from different atoms. These AOs may themselves be hybridized.

Consider the MO for the H₂⁺ molecule ion (one electron, two nuclei) or for H₂ itself. It is easy to guess the lowest-energy wave function for a single electron associated with two protons, A and B, that are VERY far apart. At any given time the electron should either look like the 1s electron of atom A (1s_A², where r is measured from A) or like the 1s electron of atom B (1s_B², r measured from B). It will certainly not spend time in the middle, where it is far from both nuclei (whatever G.N. Lewis might have thought). Of course if A and B are very far apart, it will be difficult, and slow, for the electron to get back and forth, but we are not now interested in rates, only in long-time averages. Over the long haul the electron should spend half of its time on A and half on B.

We would thus like the probability distribution to be 1/2 (1s_A² + 1s_B²).

Let's try the following guess for the MO and its probability density:

The first two terms of MO² look like what we want, but the third, the cross term, is disturbing. Not to worry! If A and B are far apart, there is no position in space where 1s_A and 1s_B are both of significant value. At least one of them will be so tiny that we can ignore the product.

What if A and B are close together, so that there is a region where the 1s_A1s_B product is significant? Then the overall size of MO² will be too large (integral greater than 1), and we'll need to replace 1/2 by something <1/2 in MO² (and thus 1/÷2 by <1/÷2 in MO). With this smaller constant the first two terms in MO² describe a superposition of the two 1s atoms with a little electron density removed. Where did the extra density go? Obviously into the region where 1s_A1s_B is significant, that is into the region between the nuclei.

But wait, this is exactly what X-ray experiments show about bonds! Bonded atoms look mostly like the atoms themselves but with a little electron density shifted to between the nuclei (as shown in deformation density maps). So this simple MO does a good qualitative job of describing reality.

With two electrons in this MO one has a description and an understanding of H₂. The electron energy it predicts is 92.9% of the stabilization of the true molecule (the difference between H₂ and separated protons and electrons), and the calculated difference between H₂ and two separated H atoms is 52% of true bond energy.

Can the description be improved? Easily. One can evaluate the quality of approximate wave functions by their average energy. Optimizing a constant in the exponent of the 1s functions (like adjusting Z_eff), which allows the atomic wave function to spread out a bit so as to increase the bonding density, improves the bond energy to 73% of experimental. Hybridizing the AOs to increase the overlap and using SCF to account for electron repulsion increases the bonding density a lot and the bond energy by a little (to 76% of experimental). Adding modest configuration interaction to keep the electrons apart results in 90% of the experimental bond energy. (click for details on these calculations)

If the energy of a pair of species (atoms, molecules, or molecular fragments) decreases by much more than about 10 kcal/mole as they approach one another we say they are chemically bonded. As far as we are concerned in this course, bonding results from decrease in the potential and kinetic energy of electrons, which makes up for repulsion between nuclei. Electrons may be thought of as occupying orbitals, each characterized by a particular spatial distribution and a particular energy, no more that two electrons to an orbital. In this way we can consider the total energy as the sum of energies of the individual electrons. In general these orbitals are molecular orbitals (MOs) and extend over the whole molecular frame. One way to approach chemistry is to try to understand what determines the energies and shapes of orbitals.

It is most fruitful to understand molecular orbitals as composed of smaller orbitals. For example, a complicated molecular orbital can be seen as a combination of two or more atomic orbitals (AOs), or as a combination of a smaller molecular orbital with an atomic orbital, or as a combination of two (or more) smaller molecular orbitals. We can view an arbitrarily complex molecular orbital in terms of the mixing of pairs of orbitals, which are themselves pairs of still simpler orbitals, until we get back, pair-by-pair, to atomic orbitals. So what we really need to understand are the rules that govern mixing orbitals in pairs.

Why should atomic orbitals mix? If one AO, A, is a little better than another one, B, why not let the electron go into A instead of into a combination of A and B? Consider an MO expressed as a linear combination of atomic orbitals (LCAO) aA + bB, i.e. a parts of A and b parts of B. Squaring it gives a²A ² + b²B² + 2abAB, which means that the electron would spend a fraction a² of its time looking like A and b² of its time looking like B. If looking like A is better than looking like B, why not make a = 1 and b = 0? Because of the 2abAB term. When b is small b² is negligible, but 2ab is more significant. The dominant effect of this term is to shift electron density within A from the side away from B to the side toward B. This does not change the electron's energy with respect to the A nucleus much, but it lowers the energy with respect to the B nucleus. Furthermore, is smooths the wavefunction, reducing its curvature and lowering its kinetic energy.

A fundamental feature of quantum mechanics is that two orbitals mix to give two new orbitals, which are as different in energy as they can be, one as low as possible, the other as high. The amount of energy shift from the old orbitals to the new ones depends on two factors:

(1) How well the original orbitals overlap

(2) How well they match in energy.

Overlap obviously depends on spatial proximity, but it also depends on the signs (or symmetry, or nodal properties) of the orbitals involved. This is why we've spent so much time worrying about the sign of ψ. For example, if an s orbital approaches a p orbital from the "side" there is no net overlap, since the positive overlap between the s orbital and the p-lobe of the same sign is exactly cancelled by its negative overlap with the other p-lobe. Such orbitals are said to be "orthogonal", and they remain independent of one another. Even in cases where there is not precise cancellation, the net overlap may be very small. Overlap also depends on orbital shapes in other, more obvious, ways. For example at the normal C-C distance π overlap between parallel 2p orbitals is considerably smaller than σ overlap between 2spⁿ hybrids that point toward one another.

Energy match depends on which atoms are involved (further right on the periodic table means higher nuclear charge and lower energy) and on which of their orbitals are being used (s lower than p, for example). When the two orbitals being mixed are quite dissimilar in energy, it is plausible (and true) that the better combination resembles the lower-energy parent both in shape and in energy, with only a slight admixture of the shape of the other parent and only a slight lowering of energy below that of the better parent. By the same token, the worse combination resembles the worse parent, than which it is only slightly higher in energy.

To a first approximation the two new orbitals have the same average energy as their parents. To a better approximation their average energy is slightly higher. Thus if both new orbitals are occupied by pairs of electrons, nothing was gained by mixing the original orbitals, and in precise fact the energy increased a bit. This makes most molecules repel one another when they get close enough for their filled orbitals to overlap significantly.

On the other hand, when there are only two (or sometimes one or three) electrons to occupy the new orbitals, there can be a lot to be gained if the lower of the new orbitals is significantly lower than either of its parents (because of favorable energy match and overlap).

Thus bonds arise from mixing a filled with a vacant orbital (nucleophile with electrophile) or mixing of two half-filled orbitals (radicals) in a situation with good energy-match and overlap. In the normal course of things filled orbitals tend to be low in energy, and vacant orbitals high in energy (that's why they're filled and vacant). So energy match can be achieved best when one molecule has an unusually low Lowest Unoccupied Molecular Orbital (LUMO), and the other an unusually high Highest Occupied Molecular Orbital (HOMO).

To find functionality or reactive sites in molecules we look at the LUMO as a possible acid or electrophilic site, and the HOMO as a possible base or nucleophilic site. There is no reason a particular molecule cannot be both an acid and a base, although it might then be prone to react with itself (e.g. borane dimerizes, formaldehyde trimerizes).

Molecules with only strong σ bonds and no unusually electronegative or electropositive atoms, and no unshared electron pairs, and no vacant valence-shell orbitals are neither acidic nor basic. They lack functional groups. Their LUMO is too high and their HOMO too low to be reactive.

To get a basic idea of bonding and reactivity in terms of orbitals, we need only count electrons and remember the following three Orbital Energy Guidelines:

1) When two non-orthogonal orbitals overlap and mix, they generate two new orbitals

one new orbital is higher in energy than either of the originals

the other is lower in energy than either of the originals

2) The amount by which the original orbital energies shift upon mixing

increases with increasing overlap

decreases with increasing energy difference between the original orbitals

3) The average energy of the two new orbitals is slightly higher than the average of the originals

Mastering these Guidelines is not a matter of brute memorization, because you know enough quantum mechanics to give the reasoning behind them.

The first two can be recalled quickly by visualizing the following diagrams. [They are based on the formula in the Box below.] The diagrams and formula ignore the difference between normalization of bonding and anti-bonding orbitals, which gives rise to Guideline 3 and makes overlap of two doubly occupied orbitals unfavorable.

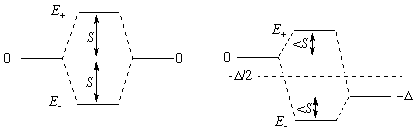
The separated orbitals have energies 0 and -Δ (in the first diagram Δ = 0).

S (roughly proportional to overlap) is how much the energies SHIFT when Δ is 0.

Of course the higher energy, E₊, comes from unfavorable (negative) overlap of the two orbitals and this MO will have an extra node. The subscript could be confusing since E₊ comes from the "difference" of the two separate orbitals [>1/÷2 (A - B)], while E_- comes from their "sum" [<1/÷2 (A + B)]. The sign given with E denotes the direction of energy shift, not the sign of the overlap.

 

You probably should remember the diagrams and ignore the formula, which is only approximate anyway. The formula is presented in hopes of making the fuzzy concepts more concrete. The formula shows that on mixing, the average energy of the orbitals stays put (BUT see Guideline 3), and that the shift from the average is larger than either S or Δ/2. The formula also shows that as Δ grows, the portion of the shift due to overlap shrinks [by a factor something like S/Δ, because for Δ>>S the ± term is about D/2 + S x S/Δ]. For Δ>>S there is very little mixing between the original orbitals. Click for Pictorial Explanation based on the Tunnelling Proton in an Harmonic Double Minimum

Because of Guideline 3, if atoms or molecules are to bond, the decrease in energy due to mixing partially filled orbitals must overcome the repulsion due to the mixing of orbitals that are doubly occupied. This repulsion is the source of "steric hindrance".

Think through the reasoning that underlies Guidelines 1 and 2. (Guideline 3 derives from the normalization condition in a way that we will not discuss in detail.)

(The idea is not to memorize all of this stuff. There are so many different combinations of orbital energies, and overlaps, and numbers of electrons, and which orbital(s) the electrons came in, that it is silly to try memorizing all possibilities. The idea is to acquire enough facility with the diagrams that you can quickly see answers to such questions.)

1) Mixing two vacant orbitals does not influence the energy of a system.

2)Two free radicals (species with singly-occupied orbitals) almost always form a strong bond. [Therefore a container full of free radicals is rare - they react with one another.]

3) Mixing a filled orbital with a vacant one is favorable as long as there is some overlap, but it is strongly favorable only when they are close in energy and have good overlap.

4) The higher the occupied orbital, and the lower the vacant orbital, the stronger will be the bond between them.

5) The orbitals to be mixed are not necessarily AOs. They can equally well be MOs, each composed of several AOs, and we can be talking about forming a new bond between two molecules rather than between two atoms.

6) Therefore the HOMO (highest occupied MO) and the LUMO (lowest unoccupied MO) play key roles in determining the bonding capability of a molecule.

7) Sometimes an apparent HOMO and an apparent LUMO within the same molecule can mix with one another to lower the HOMO and raise the LUMO, thus gaining stability and decreasing reactivity. [This is what happens to the carbonyl and amine groups in an amide, and it corresponds to resonance stabilization. Click here for an explanation.]

8) If two orbitals touch, but have no net overlap, they will not mix to give orbitals of changed energy. [This is the basis of "orbital symmetry" rules that you'll see next semester.]

9) All of the above questions have to do with the energies of the molecular orbitals. You should also think about their shapes (which AOs are large or small, where there are nodes).

Once you have all of this in hand, you are in control of the qualitative orbital theory of organic chemistry and should have no trouble identifying functional groups in molecules you have never seen before. Click here for guidance.

All that remains is to learn the lore that comes with experience of reality.