Even (perhaps
especially) if you believe in
quantum mechanics right down to your toes, you should be skeptical of
a crude, approximate application like MO theory. "Especially" because
it tries to treat strongly interdependent electrons as if they were
independent.
When we assert that you can get
some surprisingly
realistic insights from the perspective of MO theory, you should
demand examples, specific evidence that it agrees
with
reality. A great preliminary example is
Hybridization and Structure
of XH3
Molecules
Experimental Evidence
Question
Theoretical
Prediction
Facts
Evidence
from
Infrared
Evidence
from ESR -
CH3/CD3
Why
CF3 is
Pyramidal
Question:
You have often
been told that bond angles at a
carbon atom are related to its hybridization (sp linear ;
sp2 trigonal ; sp3
tetrahedral). The basis of
this relationship is that it is widely thought (not so
easily
proven) that the hybrids on a single atom
must be
orthogonal to one another, that is, they must have no net
overlap.
[It is easy to see that the overlap of two pure p
orbitals on the same atom depends on the angle between their axes. If
they are parallel (that is, if they are one and the same p orbital) the
overlap integral is 1; if they are antiparallel, it is -1 ; if they are
perpendicular, it is 0. So you will not be surprised to learn that the
integral is cos(θ), where θ is the angle
between the axes of the two p orbitals. It is a small step from here to
derive the angle between orbitals of arbitrary hybridization (e.g.
the angle between sp1.2 and sp7.3
hybrids on the same atom), but all we need to know is that there is
such a relationship. Click
here if you just must know what it is]
If we assume that bonds are
straight (which is
often true), this gives us a way of using bond angles to test our
prediction of hybridization.
For molecules of the type XH3,
there are two obvious symmetrical structures:
Planar with X
in the center of an
equilateral triangle of H atoms.
This would give 3 sp2 hybrids at 120° and a 4th,
purely p AO.
Pyramidal with
the X a certain distance
above (or below) the center of the triangle formed by the three H
atoms.
This would give angles as small as 90° (for pure p orbitals) and
leave s-character for the 4th hybrid AO.
The Question is whether
XH3 should be
planar or pyramidal for a particular X.
Theoretical
Prediction:
The X atom must
prepare itself for bonding to
three H atoms by hybridizing to give three orbitals with a
single
electron each. To prepare the best such hybrid, from the
isolated
atom's point of view, the principle is do not waste any of
the
low-energy s-orbital.
When the central atom is B,
with only 3
valence electrons, one atomic hybrid will be vacant. This lone
orbital should be p, not an sp hybrid, so as not to waste s-character.
So in preparing to bond, B should use sp2
hybridization
for the three bonding orbitals. This uses up 3 * 1/3 = all of the
s-orbital.
When the central atom is C,
with 4 valence
electrons, it makes no difference how the s-character is distributed
over the 4 hybrid orbitals. Since all four hybrids are equally
occupied and together consume all of the s orbital, none of the s-character will go to waste.
When the central atoms is N,
with 5 valence
electrons, there are 2 electrons for the nonbonding orbital. The atom
would prefer to put its s-character in this heavily occupied orbital.
Nitrogen's idea of an ideal hybridization would be pure s for the
pair and a bonding electron in each of 3 p orbitals.
But atomic energy isn't all there
is to it.
Bonding helps lower the energy of the shared electrons, especially
when overlap is good, and the best overlap for 3 orbitals
comes
with sp2 hybridization.
In two cases the prediction is
clear. By both
atomic and bonding considerations BH3
should be planar
and hard to deform out of the plane. CH3,
which
doesn't care from an atomic point of view should be planar
to
give the strongest bonds, but it should be easier to deform
than BH3.
The excitement comes with NH3.
Where the atom wants to be pyramidal while the bonds want to be
planar. Which consideration is more important? Here experiment will
teach us something, rather than just confirming our qualitiative
theory.
A very simple alternative theory for structure (but
not reactivity), Valence State Electron Pair Repulsion VSEPR, considers
only what MO theory "ignores", namely electron
repulsion. It correctly predicts planar for BH3 and
pyramidal for NH3. It also predicts pyramidal CH3.
Facts:
| XH3
| #
of Electrons in
nonbonding AO |
Atomic Hybrid
Preference | Best Overlap
for Bonding
| Observed
| Spectroscopic
Evidence
|
| BH3
| 0
| 3 x
sp2; vacant p
120°
| 3 x
sp2
120° |
"strongly"
planar
120° |
IR
1141/cm
|
| CH3
| 1
| no
preference | "
| "weakly"
planar
120° |
IR, 606/cm ESR CH3 38G
CD3
36G |
| NH3
| 2
| 3 x
p ; pair in s
90°
| " |
pyramidal
107°
| IR
932, 968/cm |
| CF3
| 1
| 3 x
sp>2 ; s>0p
<120° |
" | pyramidal
111°
| ESR
271G |
Evidence
from Infrared
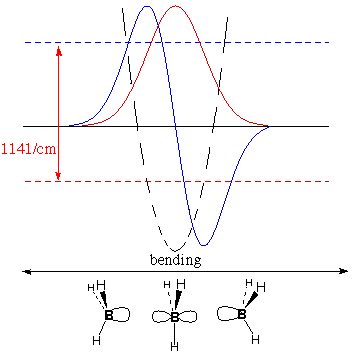
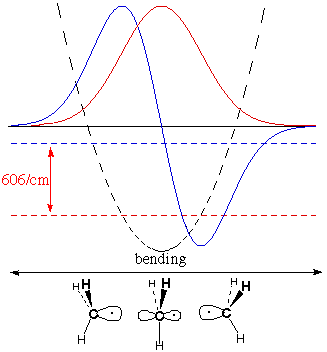
Spectroscopy
The table says that BH3
and
CH3 are predicted to be planar, and that they are
planar. How do we know this?
It is not practical to
measure the angle by
x-ray diffraction for several reasons:
(1) It is hard to find H
locations by x-ray (why?).
(2) BH3 is
a gas, not a crystal.
(3) As we'll see very shortly, BH3
molecules bond with one another to form a dimer, so BH3
doesn't even exist, except as a dilute gas. CH3
is worse. Whenever two of them get near one another their SOMOs mix to
form C2H6 irreversibly.
It is possible to observe
absorption of infrared
light by a dilute gaseous sample of BH3, or by
CH3 trapped in an inert solid at low
temperature. The IR
spectrum of BH3 shows absorption of light whose
wavelength
gives 1141 waves per centimeter (the more waves per cm, the higher
the frequency and energy). CH3 absorbs
lower-energy light
at 606/cm.
Long experience with many
molecules (and quantum
mechanical calculation) has shown that this kind of absorption is due
to the "umbrella" vibration of XH3, the
vibration that
distorts a pyramid through planarity to the mirror-image pyramid
(think of an umbrella in a high wind, or see the diagrams below the
graphs).
We can use one-dimensional
quantum mechanics to
deal with this problem, but the case is a little different from tye type
to which we are accustomed. We know the mass, but what IR give us
is
not potential
energy as a function of bond distance
but rather
energy separation of the first two quantum levels for umbrella vibration
What we need to find is the
potential energy as a
function of bending distortion. We assume it will be an harmonic
oscillator and adjust the steepness of the parabola until the energy
separation of the levels matches the IR frequency.
The figures below show for
each
molecule:
potential energy as a function of
deformation
(dashed parabola)
lowest-energy
vibrational wave
function (red nodeless wave)
energy for the lowest wavefunction (horizontal dashed
red
line)
second
vibrational wave
function (blue wave with one node)
energy for this second wavefunction (horizontal dashed
blue
line)
The
greater energy
difference for BH3,
measured by IR absorbance, shows that it meets four times more
resistance to deforming from planarity than CH3
does. This
confirms our theory that BH3 cares more about
being planar
(to leave p vacant and fully use s) than CH3
does.
But how do we know that the
potential energy
functions for BH3 and CH3
should be parabolas,
which we assumed in choosing to fit an harmonic potential? After all,
choosing a parabola assumes that the planar form is
lowest in
energy!
We don't know that they are
precisely parabolas,
but we can be certain that they are not the alternative
double-minimum displayed by NH3. The curious
thing about
the IR spectrum of NH3 is that there are
two closely
spaced lines at 932 and 968/cm rather than a single line as
in
BH3 and CH3. This results
from a double
minimum, where the planar structure is a local maximum in energy
between two pyramidal minima, as approximated below [the
simple form of the double minimum potential in Erwin
won't do
the job quite right]:
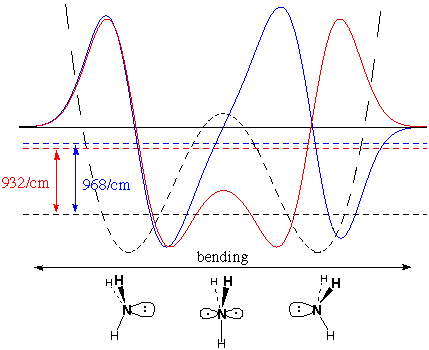
The lowest allowed total energy level (black
dashed horizontal line) represents two degenerate wavefunctions (not
shown) which are the sum and difference of nodeless functions in the
two wells.
The functions shown are the
favorable
(red)
and unfavorable
(blue)
combination of single-node, single-well functions. These are not very
different in energy, because overlap of the single-well functions is
small. The red/blue energy difference gives rise to the double
absorption of IR light, which is a certain sign that planar
NH3 is an energy maximum between the
two pyramidal
minima. Together with other data, this result shows that
NH3 is almost tetrahedral (the HNH angles are
107°
vs. 109.5° for tetrahedral), and that the planar barrier between
the two wells is about 3 kcal/mole above the pyramidal energy
minima.
Incidentally, with microwave spectroscopy it is
possible to measure the energy separation of the two lowest-energy
"out-of-plane" vibrational states for the ammonia molecule (the ones
whose energies are indicated by the single lowest dashed line in the
figure above). The difference is about 2 cal/mole (not kcal/mole) or
about 1/cm. This is obviously much less that the the difference of
about 36/cm between the third and fourth levels (where the overlap is
greater). In the lowest levels it takes ~5 x 10-14
/ 0.002 = 2 x 10-11 seconds to "tunnel" from one
well to the other. Tunneling between the excited levels is 36 times faster.
In this case the quantum theory
of molecular
vibration has been used to help interpret experimental data. It
provides a quantitative measure of molecular energetics and confirms
the geometric prediction of a very approximate (MO) form of the
quantum theory of electron distribution.
Evidence
from Electron Spin
Resonance Spectroscopy -
CH3/CD3
Other types of spectroscopy
confirm the favored
planarity of CH3. For example in ESR spectra
there is a
separation or splitting of peaks due to interaction between a
magnetic nucleus and an "odd" electron (one not existing in an
electron pair, bonding or unshared. Normally this interaction can be
observed only when the electron is actually on the
nucleus,
not just nearby. Thus splitting would be observed for an electron in
an s or sp-hybrid orbital, which has density on the nucleus, but not
for one in a pure p orbital, which has a node at the
nucleus.
There is one "odd" electron in CH3,
the
one not involved in forming one of the three bonds. In samples with a
magnetic 13C nucleus (common 12C
in not
magnetic), one can use the splitting to measure what fraction of its
time the odd electron spends in the 2sC
orbital.
The two figures below show the
odd-electron MO of
CH3 [calculated by Macspartan,
6-31G(*)] for a structure with tetrahedral
bond
angles. This orbital is often called the SOMO
(Singly Occupied
MO). In the figure on the right i the chosen
density contour has been made transparent to reveal the nuclei.
Obviously the Carbon atom lies near the node of this orbital. Because
of nonplanarity, the H 1s orbitals overlap with the mostly-2p orbital
of Carbon and create small bulges in the red lobe. This keeps the red
lobe from appearing smaller than the blue one, as one might have
anticipated for a Carbon sp hybrid that points up.
|
So in planar CH3
the electron should spend no time on the 13C
nucleus, and in bent CH3 it should spend only a
modest amount of time. As we expect the magnetic interaction measured by
EPR is small; 38 Gauss is not much compared with 400 G calculated for
an electron in a pure 2s orbital of carbon. So CH3
must be nearly planar with an almost pure 2p SOMO.
That CH3
gives even 38 G of interaction is because it is not static. Rather it
vibrates back and forth from planarity in the umbrella mode, spending
most of its time slightly bent, as you already know from the
vibrational wave function calculated above for CH3.
The reason CD3
gives a smaller splitting of 36 G, is that its heavier mass keeps the
vibrational wave function closer to planarity. |
 |
Why
CF3 is
Pyramidal
| Since CH3 is planar, one
might suppose that CF3 should be planar as well.
The F atoms have more electrons
than H, and are also partially charged because of uneven sharing of the
bonding electrons with C. On both counts they should repel one another
more strongly than H atoms do. Keeping the F atoms as far apart as
possible should favor planarity. In fact CF3 is observed by
ESR to be pyramidal. The splitting by 13C
is 272 G, 8 times as large as in CH3!
Here is the SOMO of the minimum
energy structure [calculated by MacSpartan]. The orbital contours mostly obscure the green
Fs, the black C, and the cream-colored bonds. The net contour and the
central detail show the same kind of bulge over the nucleus as in
pyramidal CH3.
| 
|
 |

|
CF3
is observed to be pyramidal, and
calculated to be so by complicated programs like MacSpartan, but how
can we understand the fact, when we predicted
planarity?
Surprising cases like this offer us the chance to learn something
new.
The explanation derives from the
poor energy-match
in the C-F bond. Whereas C and H have orbitals of about the same
energy and share bonding electrons about 50:50, the bonding orbitals
in CF3 are largely on F giving a partially ionic
bond.
Consider the Carbon atom's point
of view. In
CH3 it didn't care about hybridization, since
each of its
4 hybrid orbitals would have one electron. Each bonding orbital would
at any typical time house one member of the electron pair shared with
H. In CF3, however, the shared pairs spend most
of their
time on F, so the Carbon is not so responsible for them. The Carbon
figures, "Why not put my s orbital where it will do the most good,
stabilizing the SOMO electron, which I am mostly responsible for
(as shown above)?"
The situation is analogous to NH3,
where nitrogen is responsible for 2 electrons in its unshared pair
orbital, but only (a little more than)
one
electron in each bond. In CF3 carbon is
responsible for 1
electron in the SOMO and less than one electron in each
bond.
copyright 2001-2003 J. M. McBride