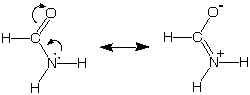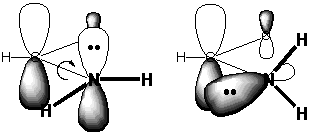We know that mixing an unusually high HOMO with an unusually low LUMO can lead to bond formation between two molecules. A similar kind of interaction can make certain molecules more stable than a naive person might think they should be. This is the so-called "resonance" stabilization.

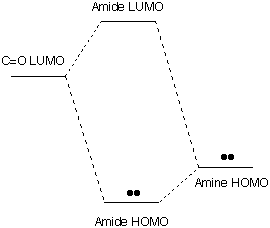
Remember our earlier discussion of the special stability of amides, a stability that we associated with our ability to draw these two more-or-less reasonable bonding pictures for this functional group. The picture on the left with complete octets and no separation of charge is expected to be a more important "resonance structure" than the one on the right, which also has complete octets but suffers from charge separation. [Here we have included two curved arrows for bookkeeping purposes to show the source of the + charge on N, the C=N double bond, and the negative charge on oxygen in the minor resonance structure.]

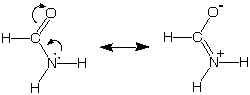
Why should our inability to draw a good single "Kekulé" picture of this molecule have anything to do with its stability?

Here again is a case of "Compared to what?"

When we say that an amide is "resonance stabilized," we mean that it is more stable than we would have expected if we thought its properties would be properly predicted on the basis of the first structure alone, so that the electronic energy would be the sum of the energies expected for an unshared electron pair orbital on N, a σ and a π bonding orbital between C and O, 2 σ N-H bonding orbitals, etc.

"Resonance energy" is rather like "correlation energy." Both are fancy names for errors we made when we chose too simple a model for reality. Both are cases where, by doing what comes naturally, electrons outsmart us and find a lower-energy home than we had built for them. [One might imagine an analogy to a public redevelopment authority that constructs a utopian housing development for individuals who turn out to be able to do a better job devising their own homes.]

When we draw the structure on the left and naively suppose that it is an adequate structure, we suppose that the energy of the molecule includes the energy of an unshared pair of electrons on N. Notice however that the C atom adjacent to this N is part of an unusually low LUMO, the π* orbital of the C=O double bond. The p orbital of the C atom is a larger contributor to the antibonding π* orbital than the p orbital of the O atom (which was mostly used up in the bonding π orbital), so there is good overlap between the π*_C=O orbital and the N lone pair.

In this simple picture there is an unusually low "LUMO" in position to overlap effectively with the high "HOMO" of the N atom. In truth the electron pair should not be unshared, as suggested by the single picture. It should be shared with the adjacent C=O group and be stabilized in the process. This is why the true molecule is more stable than we would have guessed on the basis of a single simple structural diagram.

Notice that this does not involve any crazy bouncing back and forth between two different positions for the electrons. It is just that the true molecular orbitals involve a more extensive sharing and stabilization than the simple picture envisions. It is crucial that there be effective overlap between the AOs of the carbon and nitrogen atoms to allow this special stabilization.

Think of some of the other implications of this phenomenon for the properties of proteins.
GEOMETRY : Whereas most molecules have easy rotation about single bonds, rotation about the C-N bond in amides is difficult, "because" there is a partial double bond, as shown in the ionic resonance structure. The barrier to this rotation is ~16 kcal/mole (determined by nmr spectroscopy, as we'll discuss later). Of course the real problem is that twisting about the C-N bond destroys the overlap between the unshared pair of the N and the π* vacant orbital on C, as shown in the diagram on the right. This turns off the resonance stabilization and allows us to equate the barrier to rotation with the magnitude of resonance stabilization. A second geometric implication has to do with the bonds to N. We know that the N in NH3 is pyramidal, so that the N can use some of its s-orbital character to accommodate the unshared pair. In the amide group, this pair of N electrons spends some of its time on C=O, so there is no longer as much reason for the N to use its s-character to stabilize this pair. A planar arrangement around N allows the s character to be taken from the pair and used to form stronger σ bonds to carbon and the two hydrogens. Furthermore, the N unshared pair overlaps better with C=O when it is in a p orbital than when it is in an sp~3 hybrid. Because there is no "twist" about the central C-N bond, and the N is sp2 hybridized, all of the six atoms in the core of the amide group (N-C=O and the three other atoms attached to C and N) lie in a common plane. This imposed rigidity has profound implications for the shape of proteins. There are also implications for bond lengths. To the extent that nN (nitrogen's lone pair) mixes with π*C=O, the C=O bond should be weakened and lengthened, while the C-N bond should be strengthened and shortened. These changes are suggested by the ionic resonance structure for the amide. The average C=O bond length in 481 aldehydes and ketones is 1.20Å, while that in 410 amides is 1.23Å, 0.03Å longer. The average C-N bond length in 115 amides is 1.33Å, much shorter than that the 1.47Å average of 1200 amines, but here there is a "compared to what" problem, because there is another source of shortening and strengthening for the amide - the carbon and the nitrogen atoms both use sp2 rather than sp3 hybrids in making the C-N σ bond.		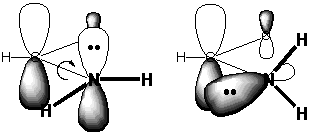Good Overlap - - - - - - - - -> Poor Overlap
REACTIVITY : The unshared pair on N, which would have been an unusually high HOMO in a normal amine, is lowered in energy, and made less reactive, by mixing with the π* LUMO of the C=O group. At the same time the unusually low π* LUMO of the C=O group, which made it acidic, is raised in energy by mixing with the occupied p orbital of N. Thus both the basic amine group and the acidic carbonyl group are made less reactive by interacting within the amide group. This is why it is much better to regard the amide group as a distinct functional group, than as an amine and a carbonyl group. The reduction of reactivity makes proteins resistant to reaction. So when you take a shower, or get a little sodium hydroxide solution on your hands, you don't have to worry about your skin dissolving.
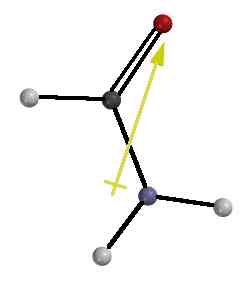
	CHARGE DISTRIBUTION : Shift of the electron pair from N to C=O gives the amide group a polar character. This polarity is indicated by the gold arrow in the figure to the left (calculated by MacSpartan Plus). The + end of the arrow shows the positive end of the electrical dipole near N and the point shows the negative end near O. [The dipole moment measured experimentally by Kurland and Wilson in 1957 is 3.71 D and is oriented at 39.6° from the C-N axis, in good agreement with the calculation. 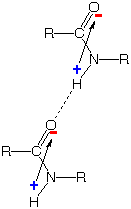This strength of dipole moment would result from shifting 1/3 of an electron's charge from nitrogen to oxygen.] Positive-negative attraction between the charges generated by this electron shift strengthens "hydrogen bonds" which hold the N-H portion of one amide group to the O atom of another, as shown on the far right. This kind of association is crucial to the formation of α-helices, β-sheets, and other "secondary" structures of proteins.

Usually we think about HOMO/LUMO mixing being intermolecular, and leading to reaction between two different molecules. Here we think of intramolecular "HOMO/LUMO" mixing as a correction to an oversimplified view of the energy, structure, reactivity, and electron distribution of a single molecule. Fortunately we can ignore intramolecular mixing for normal bonds and antibonds because overlap is small and energy-match is poor.