When we make the orbital approximation for many-electron problems, even if we use a self-consistent field treatment to try to take account of electron-electron repulsion, we are doomed to overestimate the energy because of neglecting the ability of electrons to stay away from one another by correlating their motion. We dignify this error by calling it "correlation energy." How great an obstacle will correlation energy present to our attempts to make sense out of organic chemistry on the basis of orbital ideas? If the error is tiny, we might well be justified in forgetting about it. 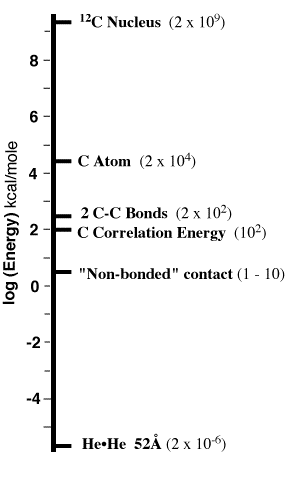So let's think about the scale of energies involved in matter and begin by taking everything apart, right down to electrons, protons, and neutrons (leave quarks for the physicists). The energies will span a range of 1015 (from 2 mcal/mole to 2 billion kcal/mole).

First we let protons and neutrons come together to form a 12C nucleus. The mass of the carbon nucleus is slightly lighter than that of its constituent six protons and six neutrons. Nearly 1% of the original mass was converted to energy when the nucleus formed. This mass defect for carbon is about 2 billion (2 x 109) kcal/mole. Nuclear energy is quite substantial!	12C atomic mass (C) Electron mass (e) Proton mass (p) Neutron mass (n) 6 p + 6 n 12C - 6 e Mass loss on forming C nucleus Energy equivalent (e=mc2)	12 [by definition] 0.0005486 1.0072765 1.0086649 12.095649 11.996711 0.098938 2.13x109 kcal/mole
		(Data from NIST)

Now we add six electrons to the carbon nucleus to make a carbon atom. This releases another 2 x 104 kcal/mole. So the electronic energy of a carbon atom is 105 smaller than its nuclear energy. A small percentage change in nuclear energy would completely swamp out any energy that is of chemical interest.	We know this by measuring the energy required for the reverse process, removing the electrons one by one from the carbon atom. Removing the first electron requires 11 electron volts of energy (multiply by 23.06 to get kcal/mole). Removing the second electron requires another 24 eV; then 48, 64, 392, and finally 490 eV for the last 1s electron. The total is 1030 eV or about 2 x 104 kcal/mole.	Ionization Potentials (eV) 11 24 48 64 392 490 Total 1030
		(Data Source)

Fortunately for us, once the nucleus is made, it stays made, and carbon nuclei do not change their energy (and mass) at all during addition of electrons to form the atom or during chemical transformations. In comparing the energy of two chemical structures, we do not have to worry about the contribution of nuclear energy, because these humongous values precisely cancel out in any comparison. We can leave nuclear energy to the nuclear physicists. (Whew!)

Now let's do chemistry by bringing atoms together to form a molecule, that is to form bonds. Carbon typically forms four bonds, each worth about 100 kcal/mole. So a typical carbon atom participates in about 400 kcal/mole worth of bonds. If we assign half of the bond energy to each of the two bonded atoms, we see that bonding generates about 200 kcal/mole per carbon atom. This is only about 1% of the electronic energy that was released on forming the atom in the first place. It is not surprising that x-ray diffraction shows that atoms in molecules look mostly like pure atoms. Bonding is an almost insignificant process compared to atom formation. This is also why it is reasonable to use atomic orbitals as a basis for describing molecules.

But for chemical transformations, bonding is the name of the game. We absolutely must get these energies right. Here's where correlation energy comes in. If correlation energy (our mistake in estimating electron energies) is of the order of 0.5% of the total electron energy, that means this error is nearly as big as bond energies!

Total Correlation Energy Prof. Wiberg, who does heavy duty computations tells me that in phenol, a molecule with 6 carbon atoms, 6 hydrogens, and one oxygen, the correlation energy is 0.36% of the energy difference between the molecule and the separated atoms. In one sense this is a very modest mistake, but it amounts to 687 kcal/mole - as much as 7 or 8 bonds!

How can we possibly tolerate such gross errors? We might be lucky the same way we were with nuclear energy. If the correlation energy (error) is identical in different arrangements of the same atoms, we can neglect it in making the energy comparisons that are at the heart of chemistry.

Unfortunately, unlike nuclear energy, correlation energy does change among different bonding schemes. So to get really precise answers one needs to do complicated calculations that go beyond SCF orbital theory. But fortunately the changes in correlation energy are modest enough that we can get very good qualitative insight into how bonding works within the orbital approximation. Changes in correlation energy during most chemical transformations are usually less than 20 kcal/mole and often much less. So as long as we can ignore errors amounting to 10 or 15% of a bond, we can use orbitals.	Correlation Energy (kcal/mole)
	Phenol H+ + Phenoxide-	687 701	Here are two examples of ionization of an organic acid. Notice that correlation stabilization is larger when there is a lone pair in a single atomic orbital (as in the phenoxide and benzoate anions) than when the same two electrons form a bond in which most of the time they are on different atoms. (Thanks to K. B. Wiberg for data and interpretation)
	Change in C.E.	14.2
	Benzoic Acid H+ + Benzoate-	977 986
	Change in C.E.	8.4

In Chem 125 we are using quantum mechanics to get a reliable qualitative idea of what bonds are and why they work the way they do. For this purpose we can put correlation energy on the back burner and go ahead to use orbitals.

(Trying to be more precise about correlation energy is somewhat futile for practical purposes, because most organic reactions take place in solution, and changes in the energy of solvation between species under comparison are sometimes as large as changes in correlation energy, or larger. Calculating solvation energy accurately is at least as challenging a problem as calculating correlation energy.)

Finally we come to a non-bonded cluster of molecules, a structure in which correlation energy plays a dominant role.

Consider the world's weakest "bond", the He-He "bond" in the helium dimer. This is certainly not a normal bond, its strength is only 2 mcal/mole (10⁸ times less than a normal covalent bond), and the average separation of the "bonded" helium atoms is 52Å, 34 times longer than 1.52Å, the length of a typical C-C bond. This is not a "molecule," just a cluster of two atoms that would quickly fall apart at temperatures above 0.001 Kelvin. No wonder helium boils at 4.2 K.

The overlap of orbitals from different atoms is energetically unfavorable when each of the overlapping orbitals starts with two electrons, for a total of four. The overlap causes two of the electrons (in the bonding "sum" orbital) to decrease in energy. But the other two electrons (in the antibonding "difference" orbital) increase in energy, a little more than offsetting the decrease in energy of the bonding pair. This should make the atoms repel one another. Of course at 52Å there is precious little overlap within the He-He dimer.

So what holds the He-He cluster together? Correlation in the motion of the electrons. Correlation energy is sufficient to overcome the predominantly antibonding SCF energy of He-He, which is of course tiny at a separation 52Å. The electrons in one He atom tend to move in such a way as to be far from the second atom when the electrons in the second atom are on the side of their nucleus near the first atom. That is, if we denote electrons by : and nuclei by O, situations A and B below are somewhat more common than C and D

(Of course it is not so likely that the two electrons of a single atom would happen to be on the same side of the nucleus. They tend to avoid one another and stay on opposite sides, but for the times when they are on the same side, A and B are more likely than C and D.)

On average this generates a weak -+ -+ or +- +- dipolar attraction between the two helium atoms that barely overcomes the repulsion caused by the almost insignificant overlapping of filled orbitals.

Analogous attraction occurs among all molecules, and it is usually stronger, because other molecules have many more electrons than the helium atom. But usually such "induced dipole" interactions are worth only a few kcal/mole, 10-100 times weaker than covalent bonding.

Although we spend most of our time in elementary organic chemistry talking about normal bonding, these weak attractions are very important in "supramolecular chemistry" and in determining the physical properties of substances (things like boiling, melting, flexibility, "recognition" of one biological molecule by another, etc.).