Two Things Wrong with Lewis's Cubic Octet
Structures

|
|
|
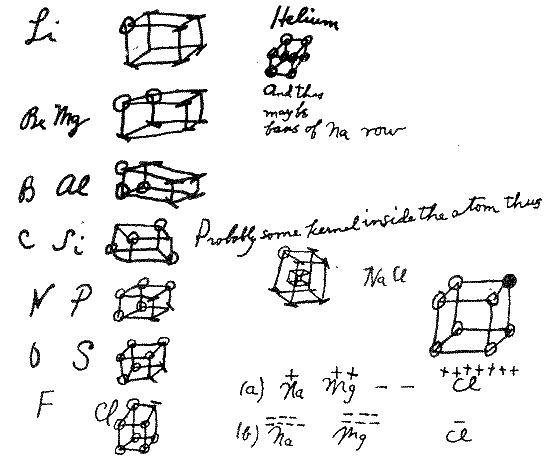
G.N.Lewis proposed the cubic octet
in 1902 as a chemistry teaching tool to give a structural
"explanation" for the periodicity of the elements in
terms of the electron, which physicist J.J. Thomson had
discovered only seven years previously. Here are his notes
from 1902.
|
|
As we will see again and again in the
course, when someone proposes a model to explain one set of
phenomena, the next step is to see if it can be used to
understand other phenomena. Lewis tried to stretch his model
for periodicity and ionic charge to rationalize the number
of covalent bonds that an atom can form - its
valence.
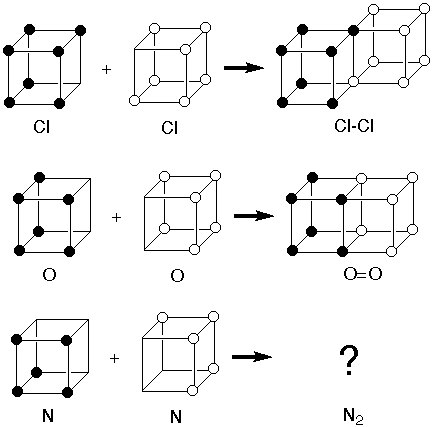
But there were two problems:
1). The
model was consistent with formation of the Cl-Cl single bond
to complete the octet of two chlorine atoms by sharing two
electrons along an edge. It was also consisent with
formation of the O=O double bond by sharing four electrons
across a face. But there was no way it was consistent with
formation of a triple bond in N2.
|
|
|
Lewis nimbly got around this
obstruction by supposing that instead of having
individual electron sites at the corners of a cube,
there were pairs of electron sites at the
corners of a tetrahedron. So two tetrahedra
could share three corners to form a triple bond.
This also seemed consistent with the previously
known tetrahedral geometry of the tetravalent
carbon.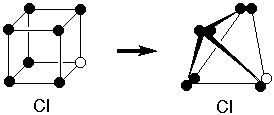
|
|
2) There is an even
more fundamental objection to the very idea of any static
structure for the atom.
In 1839 Samuel Earnshaw had proven that no system
governed by inverse square force laws (i.e. where energy is
proportional to 1/r and force, the derivative of energy to
1/r2) can possess the local energy minimum that would be
necessary if a particle is to have a stable location. Many important
forces are of the 1/r2 form. These include gravity, the
interaction between charges, and the interaction between magnetic
poles.
(Click for What are Force Laws? )
(Click for Using Lines of Force to
Prove Earnshaw's Theorem )
Lewis, like leading physicists J.J. Thomson and
James Jeans, speculated that over very small distances, such as those
within an atom, the energy of interacting charges might no longer
obey Coulomb's Law (E = q1q2/r12),
and that this would allow escape from the Earnshaw restriction. In
1923 Thomson wrote:
"… if [electron-nuclear
attraction] were to vary strictly as the inverse square of the
distance we know by Earnshaw's theorem than no stable
configuration in which the electrons are at rest or oscillating
about positions of equilibrium is possible ..."
|
"I shall assume that the law of
force between a positive charge and an electron is
expressed by the equation
|

|
"… then a number of electrons can be in equilibrium about a
positive charge without necessarily describing orbits around
it."
J. J. Thomson,The Electron in Chemistry
(1923)
(Notice that Thomson arbitrarily multiplies Coulomb's
Force Law by a factor that is essentially unity for large distance
r, but changes the sign of the force when r becomes
smaller than c, a constant which he assumed was about the
radius of an atom. This would have been brilliant, if it had only
been correct.)
In the same year the chemist Lewis
wrote:
"...if we use the electron as a test
charge to determine the properties of the simplest possible
electric field, namely the field about a hydrogen nucleus, we
appear to find that this field is not a continuum but is
strikingly discontinuous."
"Instead of thinking then of an electric
field as a continuum, we should rather regard it as an intensely
complicated mesh."
G.N.Lewis,Valence and the Structure of Atoms and
Molecules (1923)
But Lewis, Thomson, and Jeans were wrong.
Coulomb's Law does apply down to very small distances
(<10-20 times the size of an atom). A set of point
charges cannot have a stable
static
structure, cubic octet or whatever, in the absence of
non-1/r2 forces.
Of course the particles in an atom are not static.
What turned out to be wrong with classical physics as applied to such
small systems was its formulation of kinetic energy as 1/2
mv2. This was corrected just three years later in 1926 by
Quantum Mechanics, as we'll soon see when we address the true
structure of the atom.
Another Model of Shell
Structure
Like Lewis, J. J. Thomson was intrigued by
periodicity and its possible interpretation in terms of a shell
structure for electrons. Like other British physicists he loved
physical models of fundamental phenomena. He would have appreciated
Blonder's model of the shell structure for charged balls.
|
Click
here to see Blonder's 2-D
model in which electrically charged balls that repel one
another but are confined within a fixed area (through
repulsion by a surrounding charged ring) form patterns
that show shell structure. Blonder's apparatus is
described here.
|

|
[In case you're interested, the following links show how
two toys achieve levitation
by circumventing Earnshaw's (correct) Theorem: Levitron
; Diamagnetic
Levitator ]
A translation of this page into Romanian by A. Ovsov is available at http://webhostinggeeks.com/science/octet-cubicoctet-ro
A translation of this page into German by K. Bondareva is available at http://www.autoteiledirekt.de/science/zwei-dinge-falsch-mit-cubic-oktett-lewis-strukturen
copyright
© 2001,2006 J.M.McBride




