The great 19th Century chemist/physicist Michael Faraday, who was not mathematically inclined but believed firmly in facts, conceived the pictorial idea of "lines of force" which point in the direction that something is being pushed and tell, by their spacing, how strong the force is. The force is proportional to the number of lines of force that pass through a small planar surface of fixed area perpendicular to the line of force.

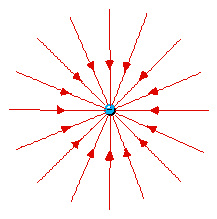
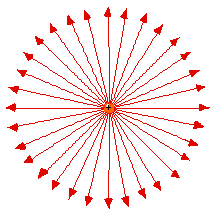
Lines of force surrounding an electron (left) and a berylium nucleus (right). Naturally the force (on a positive test charge) is toward the electron and away from Be4+. At first it seems strange that the lines of force are only twice as close together for the Be+4 as they are for the -1 electron. From Coulomb's Law one would expect four times as large a force. (click here for help on the idea of Force Laws) But these plots only show two of three dimensions. The Be4+ lines are also twice as dense in the direction perpendicular to the page. So in 3D the lines of force are indeed four times as dense.

This 2D vs. 3D geometrical argument shows why lines of force work to describe an inverse-square force law. The surface of a sphere surrounding a point charge increases in area with the square of the radius, that is the distance from the nucleus. But the same number of lines of force pass through this sphere as pass through a smaller sphere closer to the charge. The density of lines of force in 3D decreases with the square of the distance, as it must do if they are to describe an inverse-square force law.

Of course lines of force must originate on a positive charge and teminate on a negative charge, which is illustrated in the following complex diagram.

At a local energy minimum a positively charged particle would have to feel a restoring force no matter which way it is displaced. This could only be at a point where lines of force all converge. Likewise, the only stable position for a negative charge would be where lines of force all diverge. But each of these conditions is true only for a point where there is a particle of the OPPOSITE charge. By the same token, the only local energy maximum for a particle is where there is another particle of the same charge.

For a system governed by electrostatics there can be no potential energy minimum, or maximum, in an unoccupied region of space.

It is fairly easy to show mathematically that the same is true for any combination of inverse square forces (e.g. electrostatics plus gravity). This is Earnshaw's Theorem, and it explains why you are not accustomed to seeing things spontaneously levitating.

When Thompson proposed his plum-pudding model of the atom, he nimbly sidestepped Earnshaw's Theorem by putting the electrons inside a diffuse, positively charged nucleus. Curiously, our present model of the atom is precisely the opposite, with the point nucleus inside a cloud of electron density. This is fine with Earnshaw, as far as the location of the nucleus goes, but doesn't explain where the electron cloud came from. That requires motion and the curious kinetic energy of quantum mechanics.