above an infinite sheet of dipole density?
(Neglect discreteness of the dipoles. Assume continuous sheets of charge.)
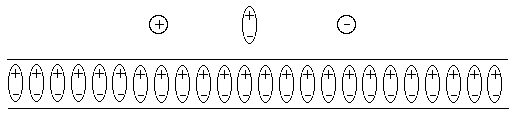
Which way is the positive charge pushed? the
negative charge? the dipole?
Is the dipole optimally oriented?
A Toy Story
The Chemical Relevance of
Earnshaw's Theorem, and
How the Levitron® Circumvents It
J. M. McBride
Department of Chemistry
Yale University
Poster presented at
Gordon Research Conference on
Physical-Organic Chemistry
June 29-July 4, 1997
E-mail j.mcbride@yale.edu
© 1997 J.M. McBride
last modified August 27, 2001
CONTENTS
1.
Earnshaw's Theorem
6.
How does Earnshaw Impact
Chemistry?
9.
What is the Levitron?
11.
How Does the Levitron Work?
13.
Vertical Stability
15.
Horizontal Stability
19.
Precession to the Rescue
20.
Limits on the Spinning Rate
21.
Acknowledgements
1. Earnshaw's Theorem
On March 18, 1839 at the Cambridge Philosophical Society Samuel Earnshaw of St. John's College read his paper:
Earnshaw questions whether the restoring force that allows particles of the ether to vibrate, as they propagate a light wave, might obey an inverse square law, like gravity. He decides no, based on a proof that depends on the divergence of such a force being zero:
Del.F = dF / dx + dF / dy + dF / dz = 0
Since they sum to zero, the restoring forces in three orthogonal directions cannot all have the same sign. There can be no local minimum (or maximum) of energy for an inverse square force law. So vibration about a point of stable equilibrium is impossible with such a force. Q.E.D.
2.
Of course Coulomb's force obeys an inverse square law, so there can be no position of stable equilibrium for a charge in a region free of opposing charges.
[A graphic proof is easily to visualize. Lines of force would have to converge on any position where a charged particle is to be in stable equilibrium, but they can converge only on a charge of the opposite sign.]
Gravitation and magnetic poles also obey inverse square force laws.
Since each of these forces alone has a divergence of zero, so must the total force resulting from any combination of them.
3.
(or maximum) of potential energy
for any set of bodies interacting by
gravitation, electrostatics,
and/or magnetostatics.
[The only critical points are saddles.]
There can be local energy minima for diamagnets (like frogs) and superconductors, but Earnshaw's Theorem forbids energy minima for permanent multipoles, even though they obey r-n forces with n greater than or equal to 4.
[For multipoles with fixed orientation the divergence of component pole-pole forces is zero. If one allows spontaneous reorientation, it becomes even easier to escape from a putative local minimum.]
There can exist local minima (but not maxima) for the total field strength, but there can be neither minima nor maxima for any single component of the field.
If there were a local maximum of total field, a favorably oriented dipole could be trapped there, but there are no local maxima.
At a local minimum, an unfavorably oriented dipole could be trapped, but it would flop over to become favorable.
When the electron was discovered (100 years ago, August 1897), Earnshaw's Theorem gave physicists headaches.
To satisfy Earnshaw with a static atom, J. J. Thompson proposed a "plum pudding" model: he planted electrons within a diffuse positive charge.
Thompson also used magnetized pins stuck in floating corks to rationalize the magic numbers of the periodic table. [J.J. Thomson, The Corpuscular Theory of Matter, Scribners, New York, 1907, p. 110ff.]
He had no way to know that in fact kinetic energy makes the electrons diffuse, so that nuclei are trapped at energy minima in the midst of a time-averaged electron cloud.
Chemist G. N. Lewis (like physicist James Jeans) suggested that Coulomb's Law might break down in order for atoms to be stable at rest while satisfying Earnshaw's Theorem.
"...if we use the electron as a test charge to determine the properties of the simplest possible electric field, namely the field about a hydrogen nucleus, we appear to find that this field is not a continuum but is strikingly discontinuous."
"Instead of thinking then of an electric field as a continuum, we should rather regard it as an intensely complicated mesh..."
[It now seems that although Coulomb's Law
fails by the Planck
length
(10-35
m), it holds at all chemically relevant
distances.]
e.g. Question:
(Neglect discreteness of the dipoles. Assume continuous sheets of charge.)

Which way is the positive charge pushed? the
negative charge? the dipole?
Is the dipole optimally oriented?
"Levitron" is the tradename of an amazing levitating top. (For examples click to visit levitron.com)
|
Roy Harrigan (Manchester, VT) counts the "Levitation Device" as one among more than 100,000 of his inventions. He built it in the late 1970's and received U.S. Patent 4,382,245 on May 3, 1983. In 1993 Harrigan gave a working prototype to Bill Hones (Fascinations, Inc. Seattle), in expectation of establishing a partnership for commercialization. Five months later Hones applied for his own separate patent, which issued on April 4, 1995. It has been estimated that Fascinations, Inc., has since sold, directly or under license, some 1,000,000 Levitrons (half of them in Japan) without Harrigan's participation. |
Roy Harrigan |
Knowledgeable physicists repeatedly told Harrigan that he was wasting his time because Earnshaw's Theorem forbids levitation of permanent magnets.
The
conditions
the Levitron must satisfy are almost impossibly stringent.
the magnet
strengths must be right;
the mass of the
top must be correct within 0.5%;
the spinning
rate must be neither too fast nor too
slow;
the top must be introduced into a
small region of
stability, only millimeters wide and high,
with
tiny translational
energy (less than required to escape a
dimple 50 microns deep).
Roy first achieved levitation spinning the top by hand in the air!
He tried spinning so often that now he catches falling objects "before I know they fell."
To a first approximation the spinning magnetic top acts as a gyroscope that stays oriented vertically in opposition to the field of the magnetic base.
But it violates Earnshaw's Theorem.
The cognoscenti know there must be more to it.
The full explanation was published by last summer by Michael Berry (Theoretical Physics, Bristol).
And independently by Simon, Heflinger, and Ridgway (Physics, UCLA)
Link to Simon et al.
The Simon et al. paper is particularly approachable for someone as mathematically challenged as I am. Both papers are important souces for this poster and present most of the information with more rigor and detail. The poster intends to serve as a qualitative appetizer to the Berry and the Simon et al. papers by providing pictures to illustrate the conditions for vertical and horizontal stability.
The force from an infinite base would be zero. At great distance the force from a finite base would be proportional to 1/r4 (as for point dipoles).
As an inverted vertical top falls toward a disk-shaped base on axis, the force opposing gravity increases to a maximum then falls to zero, as the base begins to look effectively infinite. Force is maximum at a height equal to half the base radius.
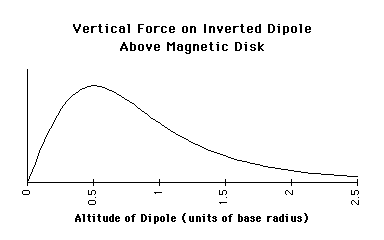
A top of small enough mass will float at an appropriate level above the height of maximum force where vertical repulsion balances gravity.
Consider the circular "footprint" of a cone originating on the top and tangent to the disk of the base magnet when the top is on the axis of the base.
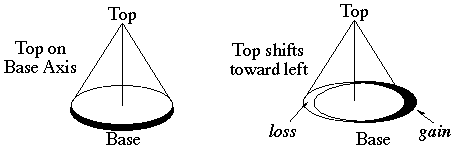
If the top drifts left, its footprint loses a small crescent from the rim of the base magnet. But the top gains an equivalent crescent of the base magnet at the right, further from the top's axis and outside the original footprint.
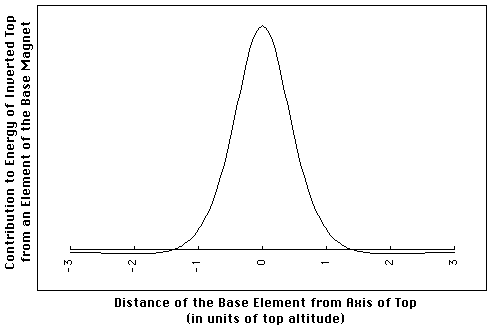
Base elements near the top's axis raise the energy. Those further from the top's axis lower it (to balance those closer in; remember, an infinite base gives no force). Beyond a certain distance the contribution decreases with increasing distance (the most favorable elements are at a distance from the top axis equal to half the top's altitude). Note that radial distance is measured in units of the height of the top.
17.
When the top is high above the base, the cone is narrow, that is, the base magnet is small measured in units of the top altitude. As shown in the graph below, the footprint is well within the steeply descending portion of the energy. When the top drifts to the left relative to the base, the crescent gained is less unfavorable that the crescent lost, and the net energy is lowered by moving off-axis.
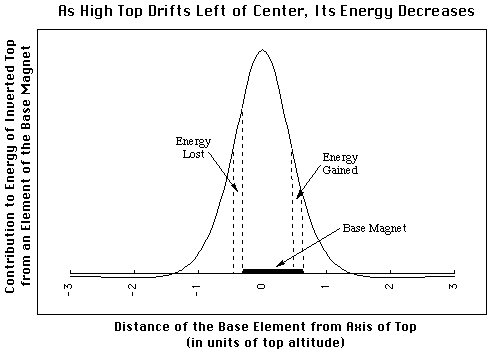
High above the base, the top experiences a destabilizing horizontal force.
A lower top would make the base effectively larger and would thus experience less unfavorable (or even favorable) energy contributions from elements near the rim of the base. If the top is low enough that the rim of the "enlarged" base extends beyond the minima at -/+ 2, there is a small horizontal restoring force on the top, because the net energy increases as the top shifts off-axis.
Near the base, the inverted vertical top experiences a stabilizing horizontal force.
The border between regimes of horizontal stability and instability comes at the same height as the border between regimes of vertical instability and stability (half the base radius, so that the rim of the base magnet is at +/-2 in the plot above, where an element's contribution to top energy is most favorable).
An inverted top that is held
strictly vertical by
gyroscopic force has no region
of overall stability.
Earnshaw's Theorem seems to forbid success of the Levitron®.
The spinning top is not held strictly vertical. It can precess about the magnetic field direction at a small angle.
As the precessing top moves off-axis, it can tilt slightly to follow the tilted local field. Since the total local field is larger than its vertical component, the tilted top experiences a small increase in total energy that increases the horizontal restoring force.
For a tilting top, horizonal stability disappears slightly above the height where vertical stability begins. Thus, there is a tiny region of absolute stability. The mass of the top must be large enough to reach vertical equilibrium below the upper limit for horizontal stability.
If the top spins too slowly, the gyroscopic torque is too small to keep it from flopping over and falling to the base.
The top can also spin too fast for stability. The precession rate is inversely proportional to spinning rate, so a rapidly spinning top does not track the local field as the top drifts off-axis. A too-fast top maintains its orientation, and Earnshaw's Theorem assures its instability.
Fortunately for Roy Harrigan, and for us, the range of stable spin rates (18-40 rps) is accessible by hand spinning.
Theory:
Michael Berry (Physics, Bristol)
Martin Simon (Physics, UCLA)
Charles Summerfield (Physics, Yale)
History:
Roy Harrigan (Inventor, Manchester, VT)
Martin Simon (Physics, UCLA)
Toy and Tolerance:
Florence McBride
J. Michael McBride
Department of
Chemistry, Yale University
Box 208107, New Haven, CT 06520-8107
e-mail: j.mcbride@yale.edu