laserdiffraction

Diffraction Demonstration

In lecture we used a helium/neon laser at the back of the classroom with lenses that expanded and then condensed its beam to focus it again to a dot on the screen at the front of the room. We inserted various objects in the region where the beam was expanded to show on the screen what their diffraction patterns look like. These examples illustrate the points made in the web page on x-ray diffraction.


The set of "benzene" slides was prepared by Professor Richard Welberry of Australian National University. The first is a set of identically oriented hexagons of dots scattered randomly over a slide. Each photomicrograph shows a very small portion of the corresponding slide.	Scattering from a HEXAGON of dots. [Actually from a large number of randomly distributed, identically oriented hexagons. It is not difficult to show that N randomly distributed patterns gives the same scattering as a single pattern but N times as intense. But it is not our business in Chem 125 to prove this.]

This second "benzene" slide shows many randomly distributed PAIRS of hexagons of dots. Some of the pairs in the top left corner are indicated by red lines added to the photomicrograph.
Scattering from a PAIR of hexagons of dots.
Interference between scattering of members of the pair generates a modulation of the original "snowflake" pattern in the direction of the repetition (up to the right).
[Actually from a large number of randomly distributed, identically oriented pairs of hexagons...]

This third "benzene" slide shows many randomly distributed PARALLELOGRAMS of hexagons of dots. Some of the parallelograms in the top left corner are indicated by red lines added to the photomicrograph.
Scattering from a PARALLELOGRAM of hexagons of dots.
Now there is modulation of the "snowflake" pattern in both directions of repetition.
[Actually from a large number of randomly distributed, identically oriented parallelograms of hexagons...]

This fourth "benzene" slide shows a regular LATTICE of hexagons of dots.
Scattering from a 2-Dimensional LATTICE of hexagons of dots.
Long-range repetition makes the "snowflake" observable only at angles where scattered waves from successive patterns are EXACTLY N waves apart (where N is an integer). Like viewing the snowflake through the holes of a pegboard. One practical advantage of the lattice (or a crystal) is that the scattered light is "focused" into the small spots, making the intensity much brighter and easier to measure.

Streched-out lighbulb filament. Divisions on the scale (which was not put in the laser beam) are 80 microns. The wire is about 75 micron diameter, the helix is about 0.4 mm diameter, and the distance between successive turns of the helix is about 0.5 mm.

Diffraction from the lightbulb filament. Note the succession of spots along the branches of an "X".

[The horizontal and vertical branches of the cross that passes through the dark "beam stop" are caused by diffraction from the rectangular window in which the filament was held. They have nothing to do with the helix itself.]

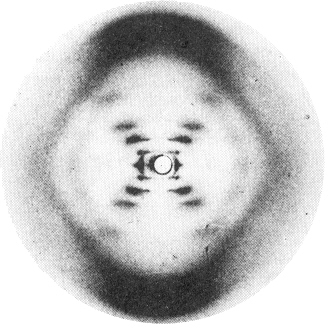
Rosalind Franklin's x-ray diffraction pattern from a sample of b-DNA that had been drawn out to align its double helices more or less vertical.

Contrast the weak-strong-strong-very weak-strong sequence of intensities along each branch of the "X", caused by the double helix, with the steady decrease of intensity in the laser scattering from the single helix

A comprehensive set of patterns and their diffraction patterns is presented in
G. Harburn, C.A. Taylor, and T. R. Welberry, Atlas of Optical Transforms, Cornell University Press, 1975

[Return to Diffraction Web Page] [Return to Chem 125 Home Page]

latest revision 9/10/05

Comments on this page are welcomed by the author.

J. Michael McBride
Department of Chemistry, Yale University
Box 208107, New Haven, CT 06520-8107

e-mail: j.mcbride@yale.edu


This second "benzene" slide shows many randomly distributed PAIRS of hexagons of dots. Some of the pairs in the top left corner are indicated by red lines added to the photomicrograph.	Scattering from a PAIR of hexagons of dots. Interference between scattering of members of the pair generates a modulation of the original "snowflake" pattern in the direction of the repetition (up to the right). [Actually from a large number of randomly distributed, identically oriented pairs of hexagons...]


This third "benzene" slide shows many randomly distributed PARALLELOGRAMS of hexagons of dots. Some of the parallelograms in the top left corner are indicated by red lines added to the photomicrograph.	Scattering from a PARALLELOGRAM of hexagons of dots. Now there is modulation of the "snowflake" pattern in both directions of repetition. [Actually from a large number of randomly distributed, identically oriented parallelograms of hexagons...]