Ever since the statistical interpretation of entropy became popular, more than a century ago, students have been taught that entropy tends to favor a state of greater disorder over a more ordered state, and that the inevitable increase in the entropy, or disorder, of the universe provides a direction for time.

A typical example is found in Richard Feynman's discussion of irreversibility [The Feynman Lectures on Physics,Vol. I, 46-7], where he uses italics to emphasize:

"It is the change from an ordered arrangement to a disordered arrangement which is the source of the irreversibility."

The truth of this sort of statement hinges on a proper understanding of what is meant by "a disordered arrangement," a meaning that may not be obvious to a naïve reader and is not always clarified (Feynman does address it several paragraphs later, see answer below).

One approach to a proper understanding of order and disorder is to consider a scientific parlor trick (one that is often analogized to spin- or optical-echo experiments). The demonstration involves Couette flow of a viscous liquid in the space between two coaxial cylinders.		Click to see the whole experiment (2 meg)
Cross Section	On the right is the first frame from a movie showing the spreading of a yellow dye in a viscous liquid (shown blue in the cross section on the left). The liquid is held between a stationary interior rod and a rotatable glass tube. In the movie the outside tube is rotated to the left by three complete turns, 3 x 360° = 1080° (note black reference line) and then rotated back again. Click to download the QuickTime movie (0.9 meg)
Compare the last frame of the movie to the first frame. Only the time on the watch has changed. (The watch proves that there has been no software hankypanky.)

THOMASINA: When you stir your rice pudding, Septimus, the spoonful of jam spreads itself round making red trails like the picture of a meteor in my astronomical atlas. But if you stir backward, the jam will not come together again. Indeed, the pudding does not notice and continues to turn pink just as before. Do you think this is odd? SEPTIMUS: No. THOMASINA: Well, I do. You cannot stir things apart. SEPTIMUS: No more you can, time must needs run backward, and since it will not, we must stir our way onward mixing as we go, disorder out of disorder into disorder until pink is complete, unchanging and unchangeable, and we are done with it for ever.

Cross Section after 1080° rotation

In fact the flow of the viscous liquid is, to a first approximation,  laminar and without turbulence, inertial flow, or diffusion. The amount of angular displacement of any bit of liquid depends only on its distance from the axis of the cylinders. The liquid has been cleanly sheared. Bits of liquid next to the rotating outer cylinder rotate with it by 1080°, while those next to the stationary inner cylinder do not rotate at all. After three cycles of rotation the dye forms a thin sheet wound three times around the cylinder axis (as shown by the red line in the cross section at the left). Viewed from the side, the dye appears to be evenly distributed, because from that perspective we cannot perceive the pattern. Reversing the rotation "unwinds" the spiral sheet back into the original line. [Of course this kind of non-turbulent "mixing" does accelerate true dissolution by shortening the distances that need to be covered by randomizing diffusion, but diffusion in a liquid as viscous as corn syrup is very slow.]

What fooled us was the appearance of randomness after 1080° rotation. The dye was just as ordered after rotation as it was before, but in a less easily perceived way.

This Couette flow demonstration makes us cautious about supposing that an arrangement is random or "disordered" just by the look of it. What appears to be disordered may truly be ordered but in a very complicated way. Of course one can arbitrarily define some quantitative measure of the randomness of a distribution (e.g. the fractal dimension), but different individuals could choose different measures. In fact any arrangement at all might be considered "ordered" by someone. Compare the two sets of 52 dots in the frames to the right. Most individuals would think of the second arrangement as rather disordered, but you can click here to see that the second is also highly ordered.

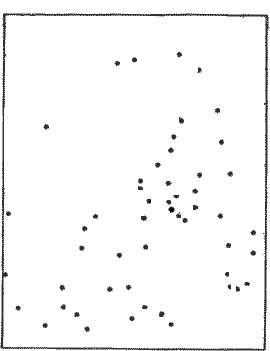
If any arrangement may be considered ordered - if order is in the eye of the beholder - the concept of "a disordered arrangement" is an oxymoron and dangerous to use in a fundamental theory.

Reversible Couette Flow as a model of spin and optical echos is discussed by R. G. Brewer and E. L. Hahn, in "Atomic Memory", Scientific American, 251, No. 6, pp. 50-57 (December, 1984) [thanks to Victor Batista for this reference]

For a more physical description of the Couette unmixing experiment see John P. Heller "An Unmixing Demonstration," American Journal of Physics, 28, 348-353 (1960).

Tom Stoppard, "Arcadia", Faber and Faber, Boston, 1993. Act I, Scene 1. [Thanks to J. D. Dunitz for pointing out this passage.]

Dinosaur connect-the-dots from http://www.lizardpoint.com/fun/java/dinodots/dino1.html