It is amazing how profoundly the turn of 1900 to 1901 marked a transition from the 19th to the 20th Century in all sorts of fields. Celebrating a centennial this December allows us to set in perspective much of what we've been studying during the fall.

In International Politics: On January 22, 1901, Queen Victoria died, ending the longest, perhaps the dourest, reign in Britain's history, nearly two-thirds of the 19th Century, and allowing her son Edward, whose love of fun extended to popular science lectures, to usher in the Edwardian era.

Trouble was already brewing with Victoria's grandson in Berlin, Friedrich Wilhelm Viktor Albert, who was both King of Prussia and Kaiser Wilhelm II of Germany. When Edward had asked Victoria to give this troublesome nephew a "good snubbing", she had replied, "Those sharp answers and remarks that only irritate and do harm and in Sovereighs and Princes should be most carefully guarded against. William's faults come from impetuousness (as well as conceit); and calmness and firmness are the most powerful weapons in such cases."

In Organic Chemistry: The previous October Moses Gomberg, an Assistant Professor at the University of Michigan, had published in Germany and in the United States a paper entitled "An Instance of Trivalent Carbon: Triphenylmethyl".

This paper marked the transition from the development of structural organic chemistry over the last half of the 19th Century, which depended on the tetravalent (and tetrahedral) nature of carbon (our subject this semester), to the development in the 20th Century of understanding how reactions occur. During a reaction that changes the set of four groups attached to a carbon, the atom must, at least temporarily, be attached to either 3 or 5 groups, so these unusual carbon valences play a key role in the reactive intermediates of "mechanistic" chemistry (our subject for next semester).

In Physics: The most profound of these three events at the turn of the century may have been a lecture to the German Physics Society in Berlin on December 14, 1900, by Max Planck, professor of physics at the University of Berlin, entitled On the Theory of the Law of Energy Distribution in the Normal Spectrum. This astounding paper changed the course of physics and set the machinery in gear for finally understanding chemistry at a fundamental level. From a chemical perspective it is worth thinking about what was behind Planck's suggestion that energy can be quantized.

Max Planck (AIP)

In 1889 Lavoisier had included light and heat (Caloric) at the head of his list of elements. But as the 19th Century came and progressed it became clear that there was a fundamental difference, besides the possession of mass, between these "imponderable elements" and the material ones: Matter was granular, energy was continuous.

The idea that matter is not smooth and infinitely divisible was prominent during the whole 19th Century. It arose in 1801, when John Dalton suggested the existence of atoms to explain the failure of gases of different density to segregate. In organic chemistry the atom concept underlay Berzelius's atomic weights (Composition), Liebig and Wöhler's radicals, Dumas's types, and Couper and Kekulé's valence (Constitution, 1858). After Cannizzaro revived Avogadro's hypothesis in 1860, everything started coming together in terms of atomic and molecular reality, although young van't Hoff's suggestion that it was meaningful to discuss the arrangement of atoms in space (Configuration, 1874) scandalized some of the older, more conservative chemists (like Kolbe). Baeyer, himself no stranger to the above concepts, refused to take seriously young Sachse's suggestion of unstrained boat and chair structures for cyclohexane (Conformation, 1889). It would be 29 years (after the structure of diamond had been determined by X-ray diffraction) before Sachse's detailed picture was accepted, but by 1900 there was already a long history of organic chemists believing in atoms.

The idea of matter being granular had also been playing an important role in physics and physical chemistry for the last half of the 19th Century, particularly in statistical thermodynamics, where gas laws were interpreted on the basis of the "kinetic theory" in which pressure resulted from the collisions of atoms or molecules with each other and with the walls of the container. In fact the average kinetic energy of the molecules (K_av) was used to define an absolute scale of temperature using the expression : T = 2/3 (K_av / k), where k came to be known as Boltzmann's constant, which was chosen to make the new temperature scale agree with the traditional Kelvin scale.

Mathematical mechanical analysis of these systems supported "Equipartition of Energy", the idea that at thermal equilibrium all atoms (or molecules) in a mixture should have the same average kinetic energy (requiring the lighter ones to be moving faster). Further mathematical analysis allowed extending the equipartition concept to other types of motion, including the rotations and vibrations of polyatomic molecules.

Statistical analysis of how energy should be distributed among molecules or oscillators led Boltzmann to his famous law showing that a "state" that is lower in energy than another one by DH should be more likely to occur by a factor of e^DH/RT (or at room temperature 10^{3/4 DH}, where DH is in kcal/mole).

Why is it "statistical" to disfavor high energies? Because if you have only so much energy to go around, it is improbable to put large amounts of it into a few molecules of high energy - better to divide the energy into many small portions that can be distributed in a zillion different ways among many molecules.

[This is closely related to why a floppy molecule, like twist-boat cyclohexane, has a statistical "entropy" factor that favors it over rigid chair cyclohexane, partially mitigating the e^DH/RT advantage of the latter. There are simply many more ways of arranging the twist-boat than of arranging the chair, in the same way that there are more gauche- than anti-butanes. For cyclohexane there are a lot more structures called twist-boat than there are called chair.] (Click for details)

In dealing with Avogadro's Number of particles, probability is tantamount to certainty.

Statistics shows that margins of error are typically proportional to the square root of the number of individuals in a sample. When the New York Times polls 900 individuals, the margin of error is 30 individuals (square root of 900), and they quote a uncertainty of 3% (30/900).
If one were to poll Avogadro's Number of molecules (6 x 10²⁴), the margin of error would be about 2.5 x 10¹², which is large as a number, but represents less that 10^-10% of the population. So in chemistry, if you know probabilities, you don't usually worry about random statistical fluctuations. That's why repeatability is a hallmark of good chemical experiments. Epidemiologists do not expect such precise repeatabililty.

Using Boltzmann's relationship together with relative energies, estimated by adding average bond energies (Ludimar Hermann, 1868), organic chemists can easily predict approximate equilibrium constants for various transformations. Nowadays such energy predictions are corrected for "steric energy" calculated by molecular mechanics (remember Chem 3D).

By the year 1900 the atomic fine structure of molecules was permanently entrenched in chemistry, though a few philosophically rigorous physical chemists (like Ostwald) and physicists (like Mach) were fighting a rear-guard action maintaining that all of this was just a handy model that had not really been proven.

Bonding had something to do with energy, but ever since the French chemists had blown dualism out of the water in the 1840s, there had existed no fundamental physical theory of bonding.

Although it was clear that matter was discontinuous, kinetic energy and heat and light seemed naturally to be continuous. You should be able put an arbitrary amount of energy into a molecule, or into a part of a molecule (like a bond vibration). Of course if you put too much in, you might blow a molecule apart.

19th Century physicists became adept at dealing not only with matter, and heat, and entropy, but also with electricity, and magnetism, and light. Here they were also making rapid progress as the turn of the century approached. It is relevant to our story that they had developed a good, fundamental electromagnetic theory of light allowing them confidently to predict how much light energy an oscillating charge of a given frequency and given average energy should emit in a given time period, and how readily it should absorb light that was incident upon it. A key feature of this theory is that the rate of light emission is proportional to the amount of excess energy in the oscillator and to the square of the oscillation frequency, while its rate of light absorption is proportional to the amount of light at the relevant frequency but independent of the value of the frequency.

Everything looked rosy, until June 1900, when the English theoretician Lord Rayleigh decided to put these ideas together to predict the amount of light at different frequencies in equilibrium with matter at a given temperature. This was the so-called "Black Body Radiation" or "Normal Spectrum".

This question had great practical as well as theoretical importance, because in 1879 Edison had invented an incandescent electric light bulb. [Actually Edison's first patent (1868) had been for an electrical vote recorder - Florida is really behind the times!] There was a lot of interest in deveoping brighter, more efficient illumination devices. In fact the Third Law of Thermodynamics was discovered by Walter Nernst, a German physical chemistry professor, in connection with his efforts to commercialize a new kind of electric lamp. [Incidentally, these efforts prospered and Nernst became so well-to-do that shortly after Gibbs's death in 1904 he gave Yale a suitable bronze memorial with a bust of Gibbs in high relief. You can see it in the main entrance to Gibbs Laboratory.]

This appeared to be a straightforward problem. Equipartition of Energy said that at equilibrium oscillators of different frequency should all have the same average energy, while light theory said that for a given energy oscillators of higher frequency should radiate more light (proportional to the square of the frequency).

If the higher frequency oscillators are radiating more light energy, but are at equilibrium, they must be absorbing more light energy as well. Since the probability of absorbing light at the relevant frequency is independent of the frequency, the only way to maintain the balance with emission is for there to be more light at the higher frequencies, which seems to be no problem, since more high-frequency light is being emitted.

Fine. Rayleigh had a clear prediction for makers of illumination devices. Heating an object should make it emit more light at all frequencies (all oscillators have more excess energy), and the amount of light energy at a given frequency should be proportional to the square of the frequency (as long as one maintains equilibrium by not allowing the light to escape - think of the light inside a heated hollow ball, where it cannot get away).

Whoa! This says that at any temperature there is more radiation at higher frequency (in proportion to frequency squared). So if there is any radiation at all in the red or infrared (low frequencies - IR frequency ~10¹³ / sec), there must be 10,000 times as much in the ultraviolet (10¹⁵ / sec), and 10¹⁰ times as much in x-rays (10¹⁸ / sec). Not to mention gamma rays. If you look at any equilibrated object (even a cold one), the x-rays and gamma rays it emits should fry your eyeballs.

This Ultraviolet Catastrophe is not only surprising, it is also untrue.

For many years researchers in many places had measured the spectrum of light emitted from heated bodies. The most recent and most precise work came from physicists at the Berlin State Physical-Technical Institute (PTR), a laboratory devoted to solving industry-related problems, who measured the overall light emission at different temperatures, the frequency of maximum emission at different temperatures, and the detailed shape of intensity vs. frequency curves at different temperatures. This was fortunate for Planck, because he was professor of theoretical physics in the University of Berlin, where he could interact closely with the PTR experimentalists.

They had been finding curves that started in the infrared and at first increased in intensity with something like the square of frequency, but, as common sense suggests, they reached a maximum and then died away at higher frequencies (see below). As a sample was heated it went from having its emission maximum in the infrared (invisible), to the red (red hot) to the blue (white hot). (Click to see the colors - but not their brightness).

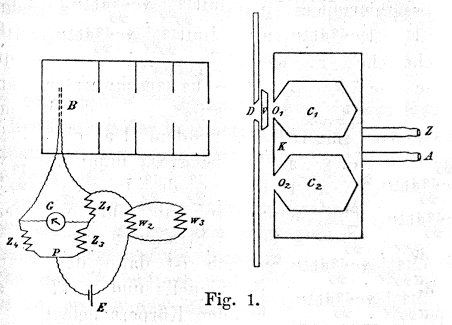
For example in 1898 Ferdinand Kurlbaum at the PTR reported that the overall radiation from a chamber heated in steam was 0.0731 watts/cm2 greater than that from the same chamber cooled in ice. He made this measurement using the setup shown in his Figure 1 on the right. The box K was filled with either steam or ice water (entering through Z, exiting through A), so the chamber c1 came to thermal equilibrium at either 100°C or 0°C. When the little shutter V (held at room temperature by circulating water and covered by velvet to keep cold air from entering c1 through o1) was pulled aside, the equilbrated light inside c1 would shine through the hole o1, and the aperture D, onto the bolometer B, which would genenerate a voltage that could be measured precisely with the circuitry at the bottom. This voltage measured the temperature of B, and showed how much light energy it was absorbing from c1 .

Others at the PTR noticed other cute things, such as Wilhelm Wien's Displacement Law. Not only does lm, the wavelength of maximum emission, shift to shorter values (higher frequency - toward the blue) at higher temperatures, it does so in a very regular way, such that the product of the absolute temperature and lm is a constant. 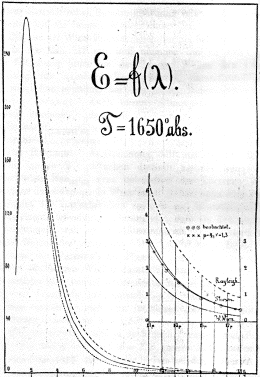Early in 1900 Otto Lummer and Ernst Pringsheim at the PTR reported a value for the Displacement Law constant: lmT = 2940 mm K The figure to the right is Lummer and Pringsheim's spectrum from a cavity heated to 1650 K. The vertical scale is light energy; the horizontal scale is wavelength (from 1 to 18 mm in the infrared region of the spectrum). Note that the maximum is at 2940/1650 = 1.78 mm   How could one understand these careful data that differed so dramatically from the predictions of "classical" physics?

(click for an enlarged version)

The first problem was to find an empirical mathematical formula that would accurately reproduce the shape of the curve of Emission vs. Wavelength for different temperatures. Wien came up with this "spectral equation" giving a formula with two empirical constants, C1 and c2, that could be adjusted to give more or less the right shape. Creating such an empirical formula has obvious utility from the industrial, engineering point of view, even if no one has any idea why it works.
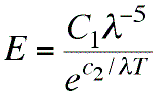
The purpose of the Lummer-Pringsheim paper of February 1900 was to show that the Wien formula wasn't quite right. It gave the lowest curve in their figure above and deviated substantially from their experimental points for long wavelengths (see enlargement on the right of the figure). They found that the recent formula of Thiesen (also at PTR) did a better job of fitting the long wavelength points in their graph,
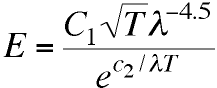
and that their own formula fitted the new points best of all. So far this was all just playing with formulas to try to reproduce the experimental curves. Some formulas fit one region of the spectrum well, some fit others, but none fit the whole spectrum well.
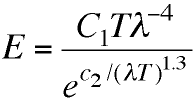
In a lecture on October 19, Planck weighed in with his own improvement of Wien's equation - subtracting 1 from its denominator. Planck admired the presence of the Boltzmann-like exponential term in this empirical equation, and the integral exponents. He said that this formula "seemed more likely to indicate the possibility of a general significance than other previously proposed formulas, apart from Wien's, which however was not supported by the facts." Overnight after Planck's lecture Heinrich Rubens, one of the PTR researchers, checked Planck's formula against the best available data, and found a good fit over the whole frequency range. Planck now tried to figure out what Nature was trying to tell him by giving a curve with this shape. He was probably not directly concerned with Rayleigh's headache, but he wanted to develop a fundamental thermodynamic theory of equilibrium that included light.

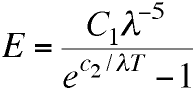
Within less than two months, he had figured it out.

The wildly incorrect "classical" prediction had been based on two theories:

Statistical Thermodynamics (Equipartition of Energy), and

Electromagnetic Theory of Light (Emission at a given frequency should be proportional to thermal energy and frequency squared; Absorption should be proportional to amount of light at the relevant frequency).

[So as not to become confused by remembering this only partially in later life, note that the total emission of light energy is proportional not to T but to T⁴, because of how the spectrum shifts with temperature. This is not relevant to the present discussion.]

If the Theory of Light is correct, Equipartion of Energy must be incorrect in predicting too much energy in high-frequency oscillators (giving rise to the Ultraviolet Catastrophe).

Why might there be less energy in high-frequency oscillators at equilibrium than equipartition predicts? Remember that statistical thermodynamics was motivated by the need to avoid putting too much energy in one place, because this would be statistically unlikely.

Suppose that you could not put arbitrary amounts of energy into an oscillator, that energy could be added to it only in units of fixed size.

i.e. suppose that, at least as regards uptake by oscillators, energy is granular (like matter).

Suppose that higher-frequency oscillators require energy to be added in larger dollops, perhaps in amounts proportional to their frequency (or maybe to the square of the frequency, or to the square root of the frequency, or something).

If this were so, any energy to be added to high-frequency oscillators would have to be added in large amounts, and populating these oscillators would be statistically unlikely for the exactly the same reason that large continuously variable amounts of energy should not concentrate in individual oscillators - just because it is not a likely situation. [Of course at really high temperatures more energy is available, and it becomes less unlikely to localize a large dollop.]

So Planck tried assuming that the energy units e that could be added to an oscillator were of size hn, where n (Greek nu) is the oscillator's frequency and h is his proposed constant of proportionality between the frequency of an oscillator and its energy unit. In a translation of Planck's words on the evening of December 14, 1900:

"We treat E however - and this is the most significant point in the whole calculation - as composed of specific number of identical finite parts and make use for that purpose of the constant of nature h = 6.55 x 10^-27 [erg x sec]. This constant multiplied by the common frequency n of the oscillators [within a given family of oscillators] gives the energy element e in ergs."

Using this assumption he redid the statistics to find the most probable energy distribution among oscillators of different frequency at a given temperature and to generate a formula that is precisely equivalent to the empirical one he had proposed on October 19, except for the translation from wavelength to frequency and the replacement of the adjustable constants C1 and c2 by meaningful ones. Notice the significance of the cube of frequency - hn for the size of the energy element, and n2 for the emission probability. To generate numbers from his new theory Planck needed only p, c the speed of light (for converting from wavelength to frequency), his new constant h (now called Planck's constant), and k (Boltzmann's constant).

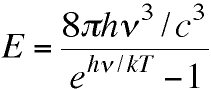
The value of p was well known, as was c (Planck used 2.995 x 10¹⁰ cm/sec, where we would use 2.998 x 10¹⁰). There were previous estimates of k, but where would he get h? By comparing his equation with experiment.

His equation showed that the maximum in the E vs. l curve should in fact obey Wien's formerly empirical Displacement Law with

So he could use Lummer and Pringsheim's l_mT = 2940 mm K to calculate h/k.

His equation also could predict k⁴/h³ from Kurlbaum's 0.0731 watts/cm² difference in radiant heat between 100°C and 0°C.

So he didn't need the previous value of k. Instead he found h/k andk⁴/h³ and solved for h and k.The values of these fundamental constants that he found in this way were correct within 1% and 2.5%, respectively! (Lummer, Pringsheim, and Kurlbaum at the PTR had done good work.)

He could check his value of k against previous values for this constant. The agreement was not too bad (though we now know that the previous values were off by 22%).

The ratio of R (the gas constant) to k turns out to be Avogadro's number N. In this way Planck found N = 6.175 x 10²³, vs. 6.40 x 10²³ by a previous method. We now know that Planck's value is better than the previous one (in fact most of the error in Planck's N comes from error in the literature value he used for R). He could check against other things too, like the value of Faraday's constant - the charge of a mole of monovalent ions.

So he was sure that he was right that, like matter, energy could be quantized.

Energy quantization was a revolutionary idea, and not surprisingly the whole world of physics did not immediately stand and salute. Most physicists ignored his theory, and Planck himself spent the next two decades trying unsuccessfully to reach the same, to him obviously correct, conclusion using the traditional ideas of physics. In 1905, five years after Planck's proposal, Rayleigh wrote "A critical comparison of the two processes [his approach and Planck's] would be of interest, but not having succeeded in following Planck's reasoning, I am unable to undertake it." But also in 1905 a very smart 26-year-old physicist seized and extended Planck's idea. Whereas Planck had only proposed that the amounts of energy an oscillator could take up had to be multiples of hn, young Einstein showed that light itself came in packets of energy hn. It was for this contribution, not for Relativity, that Einstein would be awarded the Nobel Prize in 1921. It would be another 21 years, after crucial intervening contributions by other giants including Bohr, de Broglie, Heisenberg, and many others, until Erwin Schrödinger could explain WHY, and WHEN, the energy in matter should be quantized. But the 20th Century was properly launched by Planck on a path that would lead to understanding the source of chemical bonding.

(AIP)

In 1918, the year Victoria's grandson Wilhelm II lost the First World War, abdicated his throne, and fled to exile in the Netherlands, Max Karl Ernst Ludwig Planck (1858-1947), who was just 9 months older than Wilhelm, won the Nobel Prize in Physics "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta." But Planck could not look back on this period with unalloyed satisfaction, because, widowed since 1909, he had lost his eldest son in the war in 1916, one of his twin daughters in childbirth in 1917, and the other, also in childbirth, in 1919. In 1930 Planck became President of the Kaiser Wilhelm Society for the Promotion of Science, but he suffered greatly during the Nazi years, when he remained in Germany because of his sense of duty but was openly opposed to the govenment's policies, particularly those regarding the Jews. In 1944 one of his two surviving sons, charged with participating in an attempt to assasinate Hitler, was executed by the Gestapo. Planck's home in Berlin was destroyed by Allied bombing in 1945. Planck died at the age of 89 in 1947, and the next year the Kaiser Wilhelm Society for the Promotion of Science was reestablished as the Max Planck Society for the Promotion of Science, which after more that 50 years survives and thrives as one of the world's great scientific institutions, counting more than 80 Max Planck Institutes and 15 Nobel Laureates.