Normal Intramolecular OMO-OMO Mixing (Answer)

(mixing is mostly negligible, but provides a minor lesson)

The most significant reason to ignore the mixing of filled orbitals is that it makes little difference either in total energy or in overall electron distribution. Since both orbitals are occupied before and after mixing, the decrease of energy from the favorable combination of the orginal localized orbitals is compensated by the increase in energy from the unfavorable combination. Similarly the increase in electron density in the region of overlap in the favorable combination is compensated by the decreased density in the unfavorable combination.

Furthermore since the interacting orbitals are not directed toward one another, their overlap is less that that involved in normal σ or π bonding interactions.

And, as if that is not enough, the energy of unshared pair orbitals is often significantly higher than that of normal σ bonding orbitals, so that modest overlap should give relatively little mixing.

Mixing should be least negligible when the energy match is best (as in CH3F, below), and when one is concerned with the actual energy of individual orbitals, rather than with the total electronic energy.

CH3F

For most purposes we can ignore OMO-OMO mixing between nF and a combination of σC-H bonds in CH3F. (Remember that n means unshared pair, here is is a p orbital.)

Since both orbitals are occupied, the mixing has little influence on the overall energy or electron distribution. One pair of electrons goes up in energy, one goes down. One concentrates between F and CH, the other is depleted there.

Furthermore overlap is much less than that which creates normal σ or π bonding interactions, so there is not very much shift even in the energy of individual orbitals. (Note that overlap is better for adjacent p orbitals - or for p with s - than for σ with σ.)

Of course a computer program isn't looking for the easy way out, so it goes ahead and draws the mixed orbitals shown on the right anyway, even if you'd get pretty much the same idea about energy and electron distributions by considering isolated nF and σC-H orbitals.

We do learn something by comparing these orbitals, however. Note that there is slightly less of the nF in the favorable (low-energy) combination, than in the unfavorable combination. This means that nF is higher in energy than the σC-H, but only slightly higher.

O=CH2

In the case of mixing nO with σC-H in formaldehyde, the energy match is poorer. There is much more nO in the unfavorable than in the favorable mixture, showing that nO is significantly higher in energy than σC-H.

In this case we are even better justified in ignoring the mixing of these filled orbitals.

Note, incidentally, how different the amount of mixing looks in the colored (MacSpartan) diagram from that in the black-and-white diagram. The colored contour level corresponds to a low electron density, while the black-and-white corresponds to a higher value.

Comparing these orbitals of O=CH2 and those of CH3F demonstrates the following qualitative energy relationships: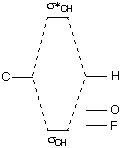

Return to Problem
Return to 125 HomePage
copyright 2001 J.M. McBride