When we said about Y for a particular structure "the magnitude of Ψ² is proportional to the probability that the set of particles with energy E will find itself in this structure", we chose the words "proportional to" carefully. Ψ² is actually probability density rather than probability.

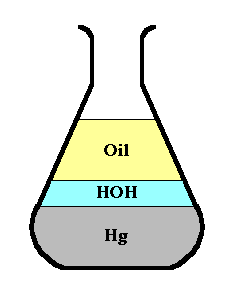
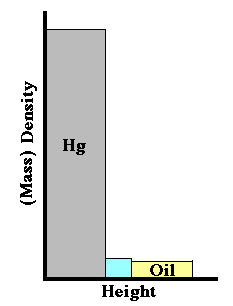
Suppose we had an Erlenmeyer flask containing mercury, water, and oil, and that we were interested in the mass within it. We could make use of the graph at the right, but the proper label for the y-axis is (Mass) Density, not Mass. To go from Density to Mass one must multiply by volume. (This is related to the old conundrum, "Which weighs more, a pound of feathers or a pound of steel?") Although the density is high at any point within the mercury layer, the amount of mass at that point is zero, because a point has no volume. You only get mass by multiplying density by volume, or integrating the density function over a volume, if the density varies with position. [Note also that the plot at the right, although correct, is misleading as to the relative masses of the three liquids. It shows clearly that there is more depth of oil than of water, and that oil is less dense, but it doesn't take into account the variation of the cross-sectional area of the flask with height. The area of a bar in the plot shows the integral of density over height, but not over volume, so it is not mass (but rather pressure).]

The same is true of probability. Suppose our quantum mechanics problem had to do with the position of an electron. For any given position, Y² gives a certain probability density, but the probability of the electron's being at that exact position is zero, because the point has no volume. To find probability we must take account of volume (either integrate the changing density over the volume in question, or choose a small volume within which Y does not change appreciably and multiply).

We could properly compare probability densities at two different points:

"The electron density in a 1s Hydrogen atom is 10 times greater at the nucleus than 0.6 Å away from it".

But to talk about absolute probability, we must specify a volume:

"The Hydrogen electron spends 90% of its time within a sphere of radius 1.4 Å", or

"The Hydrogen electron spends 5% of its time in a region between 0.5 Å and 0.6 Å from the nucleus".

For a problem involving lots of particles, the question of volume becomes pretty daunting, because the space has 3N dimensions, where N is the number of particles, but still Y² is proportional to a probability density.

For example one could properly ask,

"What is the probability that a triatomic molecule has each of its atoms within 0.05 Å of its position in a particular arrangement?"

but giving a specific answer would require integrating Ψ² over 9 variables representing x,y,z motion of each of the three atoms.

For obvious reasons, people very rarely ask such questions for polyatomic molecules. We certainly won't in Chem 125! It is more practical to compare Ψ² between two structures and say "The first arrangement is 10 times as probable as the second", when you actually mean "The first has 10 times the probability density of the second."