The number of permutations of N distinguishable objects is N! (N factorial).

This is easy to see. Any of the N objects can be in the first position, any of the other (N-1) in the second position, any of the remaining (N-2) in the third position, etc.

First pretend that the N identical bits of energy are distinguishable. Number them 1,2,3...N.

How many ways are there are putting the N bits of energy into C containers, each of which can hold any number of energy bits?

Write the contents of the containers in order, for example with N = 5 and 3 containers we could have (1 2 , 3 4 , 5)

meaning that 1 and 2 are in the first container, 3 and 4 in the second, and 5 in the third.

or

(3 , 5 2 4 , 1)
meaning that 3 is in the first container, 5, 2, and 4 are in the second, and 1 is in the third.

etc.

Let' s replace the commas representing boundaries between containers by letters, which we'll say (temporarily) can be in any order, although the first set of numbers still denotes the contents of the first container, the second set the contents of the second, etc.

So the first permutation above might be:
(1 2 A 3 4 B 5)

and the second might be:
(3 B 5 2 4 A) or (3 A 5 2 4 B)

Clearly the total number of permutations we can write for 5 numbers and two letters is:

(5+2)! = 7!
i.e. (N + C - 1)!
(the C-1 is because there are 1 fewer boundaries than containers)

There is a lot of redundancy in this way of counting permutations, because in truth we can't distinguish the bits of energy from one another, and we can't distinguish the boundaries from one another - the first boundary in the list is between the first and the second container whether we call it A or B.

To correct the counting of permutations we must divide by the number of ways of writing the energy numbers N!

and by the number of ways of arranging the boundary labels (C-1)!

So the number of significant permutations, T, is

---

THE PROBLEM

Now consider the problem we really want to address: If there are N bits of energy to put into C containers, what is the probability that there will be M bits in the first container? That is, what fraction of the total number of significant permutations have M bits in the first container?

This is easy, because if there are M bits in the first container, there must be N-M bits to distribute among the remaining C-1 containers, which can be distributed in t_M ways, where

So if the N bits of energy are distributed perfectly randomly among C containers, the absolute probability of having M bits in the first container is t_M/T, and the relative probability of having M bits is t_M.

How to deal with these factorials in the expression for t_M? We can anticipate some help from James Stirling, a Scottish mathematician and friend of Isaac Newton, whose work ~275 years ago led to the conclusion that for large N:

(The error in this approximation is about 0.1 or 4% for N = 10 and only 0.02 or 0.7% for N = 40. We are interested in MUCH larger values N, where the error is negligible.)

So we prepare to use the Stirling Approximation by rewriting the equation for t_M, the relative probability of having M bits of energy in the first container, in natural log form:

and take the derivative with respect to M (getting -1 from the chain rule when M appears in a sum):

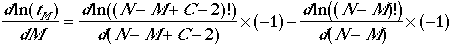
Now we use Stirling's Approximation:

The standard situation is that we have a lot more total bits of energy than containers, and that the number of bits of energy in one container is never anything like as large as the number of either containers or total bits of energy. That is, N >> C >> M or 2.

So we will make no significant error in the last fraction above if we ignore the smallest bits, M and 2, but we don't ignore C or we'd get a trivial ratio N/N.

But for small X, e^X = 1 + X, so since we are considering N >> C:

This says that a plot of the log of t_M (or in more conventional notation for probability, ρ_M), that is, the probability of having a certain number of bits of energy in a container, vs. the number of bits is a straight line whose slope is -C/N.

The probability function that fills this bill is:

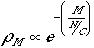
This is the Boltzmann distribution where N/C, the total number of bits of energy divided by the number of containers, or the average energy per molecule, is the Temperature measured in the same units as H, the energy of the molecule (this scaling of energy units is accomplished by the Boltzmann Constant, k).

---

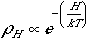
CONCLUSION

Real he-man molecular statistical mechanics has to cope with a lot of quantum mechanical subtleties, like symmetry restrictions (related to the Pauli Principle) and what exactly do we mean by "bits" of energy, but the derivation above shows where the Boltzmann Distribution comes from.

What you should remember is why it is unfavorable to put energy into a degree of freedom - that is, why ρ_H is maximum for H = 0 and decreases steadily with increasing H.

The reason is that with a given total amount of energy putting more energy into one degree of freedom decreases the number of ways of arranging the remaining energy in the other degrees of freedom of the system as a whole.

It is just a question of counting under conditions of random distribution.