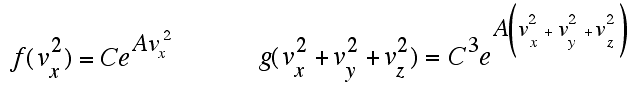In our attempt to understand the organic chemist's model of molecules by finding out where it came from, we have been emphasizing the importance of mass, the conservation of which allowed Lavoisier to launch modern chemistry on a fruitful pathway and the analytical chemists of the 19th Century to keep it going.

The other really crucial organizing principle is energy, which we are just beginning to introduce into the molecular model in terms of average bond energies and strain energies. Once energy is properly incorporated into the the model we can use it to understand structure, equilibrium, and reactivity, the most important concepts of chemistry.

During all of our previous discussions (for example in quantum mechanics) we have been making the implicit assumption that molecules "want" to be in their lowest-energy state. For example, we've assumed that a reaction will take place in order to lower the energy of the reagents (specifically to lower the energy of the electrons in their orbitals, which is why bonds form by mixing HOMOs with LUMOs or SOMOs with SOMOs).

This assumption is generally true (though sometimes adjustments are necessary to take "entropy" into account, as we'll soon see), but why? What's so great about lowering energy? Why don't molecules strive for a particular color or shape instead of for low energy? Why don't they, like industrious little entrepreneurs, strive to have more energy rather than less?

The explanation is in the realm of thermodynamics.

"Thermodynamics" does not mean "the dynamics of heat." The term was coined in the mid-1850s to describe the efforts of physicists to achieve a theoretical unification of the theory of heat with the theory of kinetic energy and mechanics. A key paper entitled "On the Kind of Motion We Call Heat" was published in 1857 (the year before valence was discovered). The idea was that heat involved the motion of particulate matter (atoms or molecules) and that when you added heat, the particles moved faster. Temperature was seen to be a measure of average kinetic energy.

At first theoreticians tried finding the average molecular velocity at a given temperature and assuming that all molecules moved with this common velocity. This didn't get very far. A great leap forward came when young James Clerk Maxwell tried using a more realistic model in which the particles in a sample could move at different velocities described by some probability distribution. He wanted to find the function f(vx) that would describe the probability in a gas at a certain temperature of finding particles with velocity vx in the x direction.	James Clerk Maxwell (1831-1879) as a Cambridge undergraduate
We are dealing again with a probability density, the same concept we encountered in describing electron distribution in space by the square of an orbital. Now we are looking at probability density as a function of velocity of an atom or molecule, rather than as a function of position of an electron. Maxwell was a very good mathematician. In 1854, when he graduated from Cambridge, he had won second place in one university mathematics competition and first in another. Now, five years later, he was able to determine the probability distribution in such a beautiful way that it is worth taking a moment to admire it, even in a course of organic chemistry.

In 1859 Maxwell wrote a revolutionary paper entitled "On the Motions and Collisions of perfectly elastic Spheres."

[This was just one year after organic chemistry was revolutionized by the proposal of tetravalence and self-linking for carbon by Alexander Scott Couper, another Scot whose birth had been within 11 weeks and 35 miles of Maxwell's]

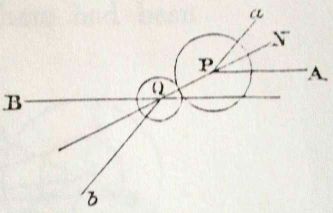
First Maxwell convinced himself that frequent random collision among particles in a gas results in velocity distributions in the x, y, and z directions that are independent of one another. That is, for a given particle the vx, vy, and vz components of its total velocity vT are independent of one another. For this purpose he drew diagrams of collision like the one at the right. Don't worry about how he demonstrated the independence. He himself worried about the argument and returned to prove the plausible conjecture in a different way some years later. Then, as shown below, Maxwell saw that in the process of saying that these three components were independent, he had in fact solved the problem of finding f(vx) ! This seems too easy, and in fact Maxwell revisited the problem later to be absolutely sure he was right.

If the probabilites of v_x, v_y, and v_z are independent, then the joint probability of having some particular set of component velocities for a particle of a given mass is just the product of the individual probabilities. That is, g(v_T), the probability of a particular three-dimenaional velocity vector v_T, must be the product of the component probabilities:

Of course something that is a function of v_x is also a function of v_x² (as long as, like this probability, it doesn't depend on the sign of v_x), so we could equally well have written (with different g and f functions):

That is, the function of a sum is equal to the product of functions of the components. There is only one function that allows you to multiply by adding. It is the exponential, where you add exponents in order to multiply. The existince of the previous relationship requires that f (and g) have the following form:

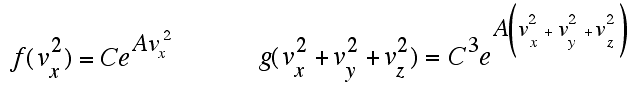
This says that, if the component velocity distributions are independent, the probability for having an x-component of velocity between v_x and v_x+ dx must be a constant (C) times e raised to the power (A times the x-velocity squared). The x-velocity squared is of course proportional to the kinetic energy, so the exponent involves kinetic energy for motion along x. Now we just need to find C and A.

The constant C just serves as a normalizing constant (as in orbitals) to make the total probability unity.

The constant A must be negative to give finite probabilities (otherwise the probability would increase without limit with increasing velocity or kinetic energy). The magnitude of A (like the Z_eff when we looked at using effective nuclear charges in atomic orbitals) determines how rapidly the exponential decays. The more negative A is, the less likely it is to have a high v_x. The size of A will determine the average value of the v_x². A is proportional to 1/T (where T is the absolute temperature) and also to the mass of the particle, so that the exponent is proportional to E_x/T, where E_x is the kinetic energy for motion along x. The proportionality constant is 1/k. So we can rewrite in terms of the kinetic energy rather than the velocity and plot the probability distribution at a high temperature (red) and a lower temperature (blue)

Note that no matter what the temperature, the most likely E_x (or v_x) is zero! For motion along x, or y, or z, or any given direction the most likely single value of the kinetic energy is zero.

In 1877 Boltzmann used a completely different approach, based on counting permutations, to show that the same exponential distribution holds for any way in which energy may be stored in a molecule (rotation about a particular axis, vibration of a certain bond, promotion of an electron to a higher-energy orbital, etc.). k in the equation above is called the Boltzmann constant.

If there are two different ways of arranging a set of atoms to give two different molecules, their relative probability at equilibrium is given by their difference in energy, ΔE: