The following table comes from Molecular Mechanics calculations on different conformations of butane (executed using the computer program Chem3DPro). The conformations are energy-minimized anti and gauche (note that the C-C-C-C angle in minimized gauche is not 60°), and the energy maxima (which we'll soon be calling passes, or transition structures, or transition states) between them.

In the second set of entries ("Relative to Anti") the values for the lowest energy (anti) conformation is subtracted to show how the others differ from it. It is worth looking at how the strain energy is distributed. There is always a give and take among different types of distortion - one can reduce van der Waals repulsion by bending or stretching bonds, for example. At first it seems curious that the order of strain energy (highlighted for gauche) is commonly torsion > bending > stretching, since the force constants are such that the amount of strain energy for a given amount of atomic motion is in the opposite order (easier to twist than to bend than to stretch). This makes sense when you think twice, because the stiffness of the higher force constants suppresses motion and most energy get stored in "softer" modes of distortion. [If this seems unnatural to you click here for an explanation.]

Below the two summary tables are the structure of the fully eclipsed conformation and a table of its individual strain contributions.

Name	anti	gauche	eclipsed	fully eclipsed
			(anticlinal)	(synclinal)
C-C-C-C Angle	180°	64.04°	119.8°	0°
Stretch	0.1542	0.1725	0.1956	0.2301
Bend	0.2977	0.6064	0.4744	1.4262
Stretch-Bend	0.0543	0.0741	0.078	0.1258
Torsion	0.0073	0.4323	2.3682	2.3168
Non-1,4 VDW	-0.4086	-0.3496	-0.3151	-0.0523
1,4 VDW	2.0688	2.1022	2.7256	2.8492
Total	2.1737	3.0379	5.5266	6.8957
Relative to Anti
Stretch	0	0.0183	0.0414	0.0759
Bend	0	0.3087	0.1767	1.1285
Stretch-Bend	0	0.0198	0.0237	0.0715
Torsion	0	0.425	2.3609	2.3095
Non-1,4 VDW	0	0.059	0.0935	0.3563
1,4 VDW	0	0.0334	0.6568	0.7804
Total	0	0.8642	3.3529	4.722

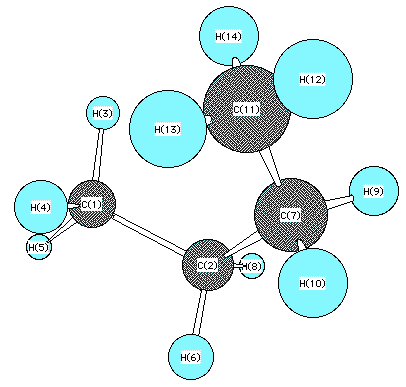
Here is a tabulation steric energy components for the fully eclipsed conformation shown (very slightly different from the model used for the composite table above) followed by the individual contributions to each components. Columns headed with K(*) are force constants for the * distortion.  Within each component the individual energies are sorted to be in decreasing order, so it is useful to look at the first few (which are Highlighted) to see which atoms they are coming from.

Stretch	0.2292
Bend	1.41
Stretch-Bend	0.1253
Torsion	2.3169
Non-1,4 VDW	-0.034
1,4 VDW	2.8495
Total	6.8968
Stretch	Length	R(0) preferred	K(S)	Energy
C(2)-C(7)	1.543	1.523	4.4	0.122	central bond
C(1)-C(2)	1.534	1.523	4.4	0.040
C(7)-C(11)	1.534	1.523	4.4	0.040
C(2)-H(8)	1.117	1.113	4.6	0.007
C(7)-H(9)	1.117	1.113	4.6	0.007
C(2)-H(6)	1.117	1.113	4.6	0.007
C(7)-H(10)	1.117	1.113	4.6	0.007
C(1)-H(5)	1.115	1.113	4.6	0.001
C(11)-H(12)	1.115	1.113	4.6	0.001
C(1)-H(3)	1.113	1.113	4.6	0.000
C(1)-H(4)	1.113	1.113	4.6	0.000
C(11)-H(13)	1.113	1.113	4.6	0.000
C(11)-H(14)	1.113	1.113	4.6	0.000
1,4 van der Waals	R	RV preferred	K(V) 1,4	Energy
H(8),H(9)	2.275	3	0.047	0.692	eclipsed Hs	These strains have
H(6),H(10)	2.276	3	0.047	0.690		been reduced by
C(1),C(11)	2.908	3.8	0.044	0.402	eclipsed Cs	stretching/bending
H(9),H(12)	2.484	3	0.047	0.227
H(5),H(8)	2.486	3	0.047	0.224
H(5),H(6)	2.486	3	0.047	0.224
H(10),H(12)	2.488	3	0.047	0.222
H(10),H(13)	2.531	3	0.047	0.166
H(4),H(6)	2.532	3	0.047	0.164
H(3),H(8)	2.533	3	0.047	0.164
H(9),H(14)	2.534	3	0.047	0.162
C(2),H(14)	2.915	3.34	0.046	0.029
C(7),H(3)	2.917	3.34	0.046	0.028
C(7),H(4)	2.918	3.34	0.046	0.028
C(2),H(13)	2.919	3.34	0.046	0.027
H(6),H(9)	2.89	3	0.047	-0.034
H(8),H(10)	2.89	3	0.047	-0.034
C(2),H(12)	3.566	3.34	0.046	-0.051
C(7),H(5)	3.566	3.34	0.046	-0.051
C(1),H(9)	3.358	3.34	0.046	-0.053
C(1),H(10)	3.359	3.34	0.046	-0.053
C(11),H(6)	3.358	3.34	0.046	-0.053
C(11),H(8)	3.359	3.34	0.046	-0.053
H(3),H(6)	3.104	3	0.047	-0.054
H(4),H(8)	3.104	3	0.047	-0.054
H(9),H(13)	3.104	3	0.047	-0.054

H(10),H(14)	3.105	3	0.047	-0.054
Non 1,4	R	R preferred	K(V) non 1,4	Energy
H(3),H(14)	2.367	3	0.047	0.196	Hs on opposing
H(4),H(13)	2.376	3	0.047	0.183	methyl groups
C(1),H(14)	2.848	3.34	0.046	0.052	(Also reduced by
C(11),H(3)	2.852	3.34	0.046	0.049	stretching/bending)
C(11),H(4)	2.853	3.34	0.046	0.049
C(1),H(13)	2.857	3.34	0.046	0.047
H(5),H(12)	5.126	3	0.047	-0.005
H(5),H(9)	4.224	3	0.047	-0.016
H(5),H(10)	4.225	3	0.047	-0.016
H(6),H(12)	4.225	3	0.047	-0.016
H(8),H(12)	4.223	3	0.047	-0.016
H(5),H(13)	3.924	3	0.047	-0.023
H(4),H(12)	3.921	3	0.047	-0.023
H(3),H(12)	3.918	3	0.047	-0.023
H(5),H(14)	3.915	3	0.047	-0.023
H(8),H(13)	3.88	3	0.047	-0.026
H(3),H(10)	3.877	3	0.047	-0.026
H(4),H(9)	3.877	3	0.047	-0.026
H(6),H(14)	3.875	3	0.047	-0.026
C(1),H(12)	4.018	3.34	0.046	-0.034
C(11),H(5)	4.018	3.34	0.046	-0.034
H(4),H(10)	3.437	3	0.047	-0.042
H(6),H(13)	3.438	3	0.047	-0.042
H(3),H(9)	3.436	3	0.047	-0.042
H(8),H(14)	3.436	3	0.047	-0.042
H(4),H(14)	2.978	3	0.047	-0.054
H(3),H(13)	2.988	3	0.047	-0.054
Angle bend	Angle	preferred	K(B)	EBend	K(St-Bend)	ESB
C(2)-C(7)-C(11)	116.408	109.5	0.45	0.471	0.12	0.0652
C(1)-C(2)-C(7)	116.408	109.5	0.45	0.471	0.12	0.0652
H(6)-C(2)-H(8)	105.65	109.4	0.32	0.099
H(10)-C(7)-H(9)	105.646	109.4	0.32	0.099
H(12)-C(11)-H(13)	106.961	109	0.32	0.029
H(4)-C(1)-H(5)	106.964	109	0.32	0.029
H(3)-C(1)-H(5)	106.982	109	0.32	0.029
H(12)-C(11)-H(14)	106.984	109	0.32	0.029
C(7)-C(11)-H(14)	111.609	110	0.36	0.020	0.09	0.0042
C(2)-C(1)-H(4)	111.602	110	0.36	0.020	0.09	0.0042
C(2)-C(1)-H(3)	111.588	110	0.36	0.020	0.09	0.0042
C(7)-C(11)-H(13)	111.582	110	0.36	0.020	0.09	0.0042
C(11)-C(7)-H(9)	107.977	109.41	0.36	0.016	0.09	-0.0051
C(1)-C(2)-H(6)	107.984	109.41	0.36	0.016	0.09	-0.0051
C(1)-C(2)-H(8)	107.998	109.41	0.36	0.016	0.09	-0.005
C(11)-C(7)-H(10)	108.003	109.41	0.36	0.016	0.09	-0.005
C(2)-C(1)-H(5)	110.755	110	0.36	0.005	0.09	0.0022
C(7)-C(11)-H(12)	110.754	110	0.36	0.005	0.09	0.0022

C(2)-C(7)-H(9)	109.117	109.41	0.36	0.001	0.09	-0.0016
C(7)-C(2)-H(6)	109.129	109.41	0.36	0.001	0.09	-0.0016
C(7)-C(2)-H(8)	109.143	109.41	0.36	0.001	0.09	-0.0015
H(3)-C(1)-H(4)	108.732	109	0.32	0.001
C(2)-C(7)-H(10)	109.157	109.41	0.36	0.001	0.09	-0.0014
H(13)-C(11)-H(14)	108.732	109	0.32	0.001
Torsions	angle	V1	V2	V3	E torsion
C(1)-C(2)-C(7)-C(11)	0	0.2	0.27	0.093	0.293	All these
C(1)-C(2)-C(7)-H(9)	-122.469	0	0	0.267	0.266	values
H(6)-C(2)-C(7)-C(11)	-122.484	0	0	0.267	0.266	involve
C(1)-C(2)-C(7)-H(10)	122.535	0	0	0.267	0.266	torsion
H(8)-C(2)-C(7)-C(11)	122.518	0	0	0.267	0.266	about the
H(6)-C(2)-C(7)-H(10)	0	0	0	0.237	0.237	central (C2-C7)
H(8)-C(2)-C(7)-H(9)	0	0	0	0.237	0.237	bond.
H(6)-C(2)-C(7)-H(9)	115.05	0	0	0.237	0.233	They sum to
H(8)-C(2)-C(7)-H(10)	-114.95	0	0	0.237	0.233	2.3 kcal
H(9)-C(7)-C(11)-H(13)	-175.683	0	0	0.237	0.003
H(4)-C(1)-C(2)-H(8)	175.923	0	0	0.237	0.003
H(3)-C(1)-C(2)-H(6)	-176.009	0	0	0.237	0.003
H(10)-C(7)-C(11)-H(14)	176.241	0	0	0.237	0.002
H(9)-C(7)-C(11)-H(12)	-56.638	0	0	0.237	0.002
H(5)-C(1)-C(2)-H(8)	56.864	0	0	0.237	0.002
H(5)-C(1)-C(2)-H(6)	-56.941	0	0	0.237	0.002
H(10)-C(7)-C(11)-H(12)	57.165	0	0	0.237	0.001
H(9)-C(7)-C(11)-H(14)	62.442	0	0	0.237	0.001
H(3)-C(1)-C(2)-H(8)	-62.2	0	0	0.237	0.001
H(4)-C(1)-C(2)-H(6)	62.115	0	0	0.237	0.001
H(10)-C(7)-C(11)-H(13)	-61.873	0	0	0.237	0.001
C(2)-C(7)-C(11)-H(13)	61.26	0	0	0.267	0.000
H(3)-C(1)-C(2)-C(7)	60.913	0	0	0.267	0.000
H(4)-C(1)-C(2)-C(7)	-60.966	0	0	0.267	0.000
C(2)-C(7)-C(11)-H(14)	-60.62	0	0	0.267	0.000
H(5)-C(1)-C(2)-C(7)	180	0	0	0.267	0.000
C(2)-C(7)-C(11)-H(12)	-179.684	0	0	0.267	0.000

If the concept of storing more energy in the easier distortion seems funny to you, think of hooking a rubber band to a suspension spring of a Mack truck and pulling on the end. The rubber band would stretch and the spring wouldn't, so all the energy would go into the rubber band. If you want to be more concrete and quantitative, think of it this way:

The force on a spring depends on how much it is stretched (dx). The energy stored in the spring depends on the square of the distortion (this is why the potential for an harmonic oscillator is a parabola). Where k is the spring constant,

F = -k dx ; E = 1/2 k (dx)²

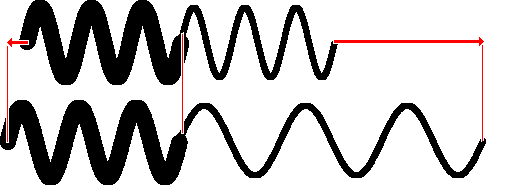
When two springs interact, as when you hook a weak spring ( k₂) to a strong spring ( k₁ = 8 x k₂) and pull on the two ends, the force on the two springs is the same, so the weak one stretches more (here 8 times as much):

F₂ = (-)F₁ means that k₂ dx₂ = k₁ dx₁ means that dx₂ = 8 dx₁

This means that the weaker spring stores 8 times as much energy as the stronger spring (k is 8 times smaller, but dx² is 64 times larger).

In summary: since the forces must balance, more energy goes into the weaker spring.